Download this chapter for offline viewing (no videos, 1MB)
Download this chapter for offline viewing (includes video content, 22MB)
Gravitational systems act from a point of central attraction. This central force causes the outward movement of the Universe to slow. The slowing Universe reduces the velocity of light, and the greater dispersion of mass reduces the acceleration rate. Throughout this incarnation of the Universal Black Hole the velocity of expansion and the deceleration rate have stayed in balance so the Universe is expanding at its exact escape velocity.
Mass and the Universal Black Hole
The mass of the Universe resides on the surface of the Universal Black Hole. The radius of the Universe is continually expanding at the velocity of light. The interior of the Universal Black Hole is when the Universe was younger and at lesser radii. The center of the black hole is the Big Bang itself.
Stated another way, all mass resides in the universal present. This present is the current radius. This mass is moving away from the Big Bang center at c. Every passing second the distance from that center increases 300,000 km.
The Universal Black Hole surface is appropriately called the event horizon. The time frame known as the present is the creation of new events. The event horizon is where all events are generated. Once created, these events and their fixed location in spacetime retreat into the past to be left behind the expanding present.
Acceleration
What is acceleration? Velocity is a change in space over a change in time or ds/dt. Acceleration is the change of velocity over time, that is:
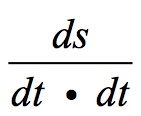
Velocity as opposed to speed is a vector function. It can be symbolized by
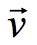
but the vector nature of velocity is understood making this symbol unnecessary.
The overall speed can be maintained but the direction changed. This change is an acceleration. Velocity can be slowed. This too is an acceleration, contrary to our perceptions when braking an automobile. The brake becomes the opposing vector to the speed of the vehicle.
Objects have inertia. Classically, inertia has been described: “An object at rest tends to stay at rest, while an object in motion tends to stay in motion”. Inertia is a vector function so like velocity a change in its vector is acceleration. Inertia affects acceleration necessary to change velocity. The greater the mass, the greater the proportional acceleration.
Force and Acceleration
There are four fundamental forces in nature. These are gravity, electromagnetic force, weak force, and strong force. These forces govern interactions within the Universe. Gravity is the most pervasive force for it acts over great distances. Its strength pales compared to that of the other three forces, but unlike its brethren, gravity operates over great distances and is not cancelled locally by opposing charges. Therefore, of the four forces, gravity alone changes motion within the macro-universe. That change in the motion vector is acceleration.
What is the Mechanism of Gravity’s Acceleration?
General Relativity established that spacetime is warped near large masses. It states that its effects result from this curvature. The path that other masses follow relative to that central mass is based upon this curvature rather than that of a traditional force.
This leads to the question, how does gravity, or any force, convey its effects? Force conveyers are bosons. With gravity that boson is the theoretical particle called the graviton. What happens locally to cause spacetime’s curved pathways?
The Schwarzschild metric formulates the movement of time within the proximity of a massive object.

where:
| dτ | = the flow of local time |
| dt | = the flow of distant time, i.e., flat spacetime |
| RS | = the Schwarzschild radius, i.e., the radius of the event horizon if mass were compressed to a black hole |
| r | = the radius of the observed mass |
| dr | = the change in radial movement |
| dΦ | = the change in angle of tangential movement |
The first part of the formula
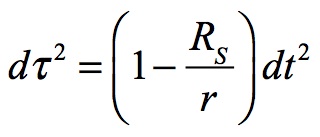
isolates the time relationship of the flow of local time in a shell location near a massive astronomical body. The shell is a conceptual spherical layer of a specified radius r from the mass’ gravity center. Local time dτ, sometimes called wristwatch time, slows relative to time at a great distance from that mass, i.e., flat spacetime (dt). Movement in space through dr or rdΦ also affect local time.
What this shows is that local time slows down relative to a distant observer as a mass moves progressively closer to Schwarzschild’s radius. This shows that time flow is layered based upon the shell from which it is measured.
The question becomes, is this layering the impetus that causes gravity’s attraction, or is it only a consequence of that attraction? If the time layering is the mechanism of attraction, then we have part of the solution to how gravity works or even possibly how all forces function.
Acceleration then becomes the proportional change in the layering of these shells. The greater the time differential over a unit of radial distance from a gravitational center, the greater the acceleration. Objects are accelerated from faster time flow to slower. Following the Schwarzschild formula, it is the d of radius (r) that determines acceleration. The derivative is the limit of the smallest increment possible.
Acceleration of the Universe Under General Relativity
The acceleration rate of the Universe is that of a mass at the event horizon of a black hole with the radius of the Universe. Note that acceleration can mean towards increasing velocity or decreasing velocity. It is just a matter of vectors. The Universe is decelerating, but the force causing this deceleration is an accelerating force.
Acceleration is the first derivative of velocity. If neutral-energy1 freefall velocity is:
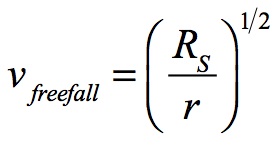
Then g becomes the first derivative of that velocity:
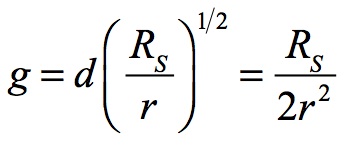
This expresses acceleration in geometric terms. To change this to conventional units RS/2r2 must be multiplied by c2:
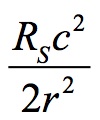
When this is converted to the acceleration for the Universe (A), the formula becomes:
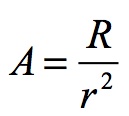
The expansion of the Universe is the expansion of the event horizon of the Universal Black Hole. The horizon of the Universal Black Hole is r = R therefore:
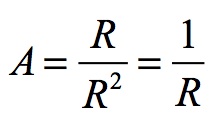
This is converted to convention units by multiplying by c2:
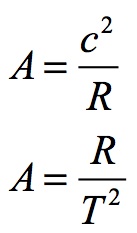
When the radius of the Universe and its age are entered into this formula, the Universe’s acceleration becomes:
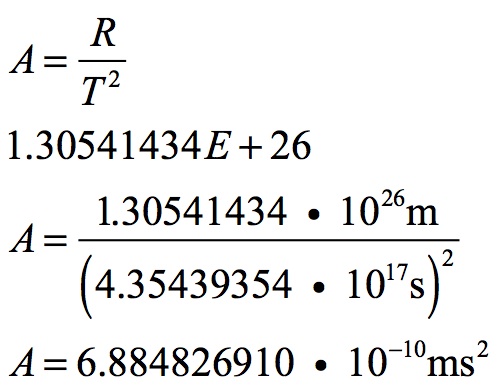
This means that the Universe is slowing down by 6.8848269 • 10-10ms-2. This shows up in the decelerating velocity of light.
The formulas for the change in the velocity of light relative to the changing radius of the Universe have already been established. To determine how fast the Universe’s expansion is decelerating, we can take the velocity of light for this moment and for this time in its expansion and then recalculate the velocity of light after adding a year. The following is a calculation of this change:
| Calculation of the Change in the Velocity of Light Per Annum | |
|---|---|
| Velocity of Light | 2.9979245800E+08 m/s |
| Seconds to a Year | 3.1558150000E+07 s |
| ΔT = T2 – T1 = 1 | 1.0000000000E+00 yr |
| T1 = Universe’s Age (T) | 1.3798000000E+10 yr |
| T2 = T + 1 | 1.3798000001E+10 yr |
| T1[s] = T1[yr] • (3.155815 • 107 s yr-1) | 4.3543935370E+17 s |
| T2[s] = T2[yr] • (3.155815 • 107 s yr-1) | 4.3543935370E+17 s |
| Proportionate Change T [yr] | 1.0000000001E+00 |
| (Proportionate Change T) – 1 | 7.2474248825E-11 |
| R1 | 1.3054143400E+26 m |
| R2 = (T2/T1)2/3R1 since T2 = (R2/R1)3/2T1 | 1.3054143401E+26 m |
| Proportionate Change R | 1.0000000000E+00 |
| (Proportionate Change R) – 1 | 4.8316239898E-11 |
| c1[s] = R1/T1m s-1 | 2.9979245764E+08 m s-1 |
| c2[s] = R2/T2m s-1 | 2.9979245764E+08 m s-1 |
| Δc = c2 – c1 | -7.2423815727E-03 m s-1 |
The velocity of light changes by 7.24 millimeters per second per year. Over ten or twenty years, this velocity change should be large enough to measure. The problem is that it may not be that simple to observe. The velocity of light is different on Earth than it is in orbit. The instruments used to measure the velocity will show the same result since the flow of time changes in proportion in each measured reference frame. What shows up is the different time flow as measured by atomic clocks.
The change in the velocity of light might also have effects on emission wavelengths thus affecting measuring devices. The faster time flow that changes light’s velocity also affects all time-based physical effects.
Wavelengths vary with changing flows of time, but what does not change is distance. It has already been shown that Planck’s distance is fixed for all time, under all reference frames. Any experiments undertaken to measure light’s velocity need to rely on this constant.
The changing velocity of light also changes the light-year. This calculation shows that the light year declines by -285,560 meters per year. This makes the Universe more inaccessible due to the shortening light year measuring stick.
| Calculation of the Change in Light-Year | |
|---|---|
| LY1 = c1 • s yr-1 | 9.4608953472E+15 m yr-1 |
| LY2 = c2 • s yr-1 | 9.4608953469E+15 m yr-1 |
| ΔLY = LY1 – LY2 | –2.2855600000E+05 m yr-1 |
Flat Universe
Prior to the late 1990s it was believed that the Universe was slowing due to the action of gravity. The question became whether the Universe was open, flat, or closed. For the Universe to be flat the mass density and the expansion momentum had to be precisely at the critical balance point. This is somewhat akin to balancing a pencil on its point.
That the Universe is a black hole changes the entire picture. The Universe is flat, i.e., it is expanding at its exact escape velocity. The mandatory acceleration rate at the event horizon is g = c2/R. The velocity at the event horizon by definition is c. At the horizon g is the exact acceleration rate to counter an outward velocity of c. With the Universal Black Hole, A is the exact deceleration rate to keep the Universe flat, i.e., expansion = escape velocity.
The discussion of whether the Universe is accelerating, open, closed or, by some off chance, flat becomes moot under the Universal Black Hole model. The Universe is flat because the physical laws are a product of this flatness. If the balance between velocity and acceleration changed, so would the resulting laws.
Acceleration to a Black Hole Versus the Acceleration of a Black Hole’s Horizon
It has been established that the Universe is a black hole and is designated as the Universal Black Hole. But the UBH contains individual black holes within its spacetime. This can be confusing, but it is an essential part of this theory. The existing paradigm for how black holes affect the Universe around them differs from the Occam’s Razor model. The following explains that difference:
Acceleration Towards a Black Hole (Within This Universe)
An object’s rate of acceleration towards a large mass reaches infinity at the event horizon of a black hole. The velocity of approach to that horizon increases until at that horizon it becomes that of light. Wristwatch time slows down with velocity so at the velocity of light wristwatch time slows to zero. The resulting acceleration from a freefall to the horizon increases without limit since the time experience of the freefall mass slows towards zero.
Time flow in the curved spacetime of a massive object relative to time passage in flat spacetime is slowed due to two effects: 1) the proximity of the passing shell to the event horizon of a freefall mass, and 2) the special relativity effects incurred by the high velocity relative to the shell passed.
Since each shell’s time dilation is proportional to the distance from the horizon, each incremental radial advance causes an accelerating slowdown of the experienced time flow according to the time portion of Schwarzschild’s metric:
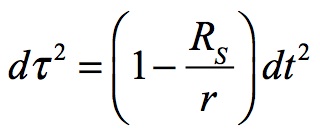
As r approaches RS,
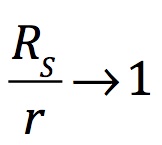
and
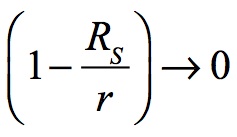
Acceleration is based upon the change in space divided by the square of the change in time. The rapidity of the factor
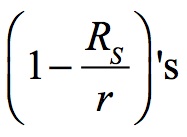
approach to zero accelerates for each passing shell since this factor is a proportional move towards the critical RS radius. For example, when r is 5.0 RS and declines to 4.9 RS this 0.1 decline changes time’s flow much less than when moving from 1.5 RS to 1.4 RS. In the first example the radial change of 0.1 r changes the factor by 0.004082:
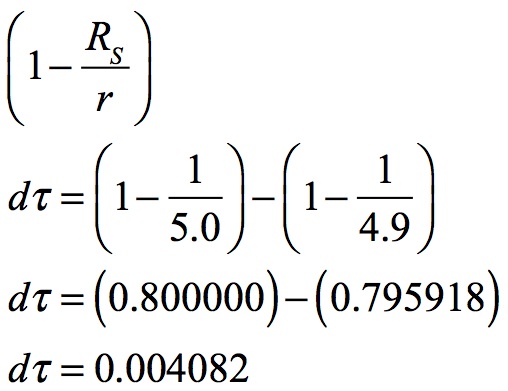
While the same 0.1 RS advance inward from a 1.5 RS changes the factor by 0.047619. The proportional time flow change for the inner shells is almost 12 times greater.
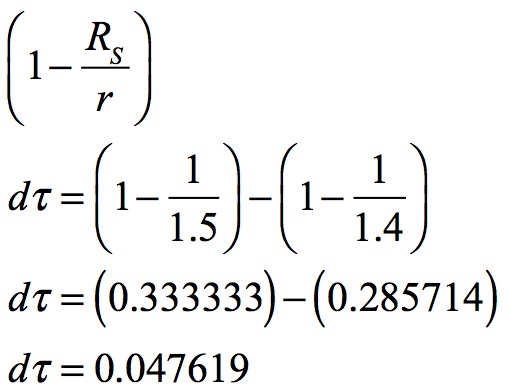
The second dynamic that affects acceleration is based on Special Relativity. The slowed time experience due to the velocity of a freefall mass passing a local shell enhances the General Relativity’s curved spacetime effects. Going from 99.9990% of the velocity of light to 99.9999% c is only a 0.0009% acceleration as measured by a passing fixed-shell observer, but it is a 316% acceleration to the free-fall mass due to Special Relativity’s greatly slowed time flow. For each additional percentage 9 there is a commensurate 316+% acceleration experienced by the freefall mass.
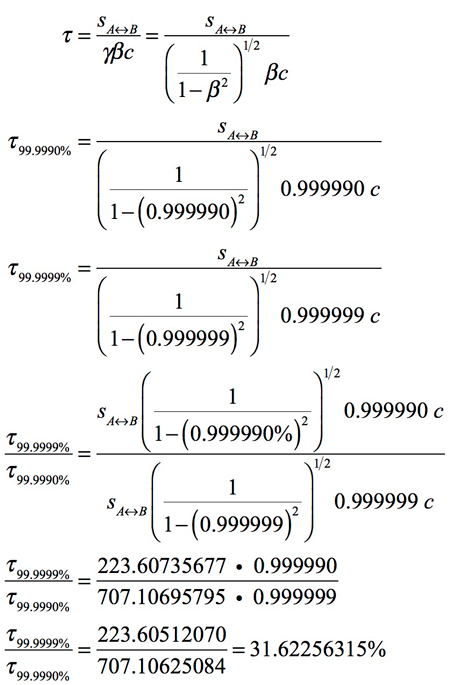
If it takes the particle 31.623% less wristwatch time to travel a specific distance between two fixed locations, it has experienced a 316.223% change in its effective velocity.
While a shell observer would not witness this change in velocity, he would observe a 316.2% increase in the particle’s locally measured energy.


If the particle is accelerated from 99.9990% to 99.9999% of c, it will experience a 316.2% change in velocity over the proper time it takes to make the change. This is the acceleration experienced by the particle.
In General Relativity the fixed shell observer’s view of a passing freefall mass would be the equivalent of the lab technician’s vantage point for a particle accelerator. If it is assumed that the mass is freefalling at neutral energy, the shell observation of the mass’s velocity would be (RS/r)1/2 • c, where c is the local velocity of light for the shell observer.
Acceleration is based upon the change in space divided by the square of the change in time. Time flow squared is in the denominator. So as a mass moves through progressively closer shells, the slowdown in time flow relative to a mass in flat spacetime, progresses exponentially until at the last Planck shell above the horizon time flow moves to zero dτ→0 causing acceleration in that last shell to move to infinity, i.e., dr/dτ2→∞.
Acceleration Towards a Black Hole (Within This Universe)
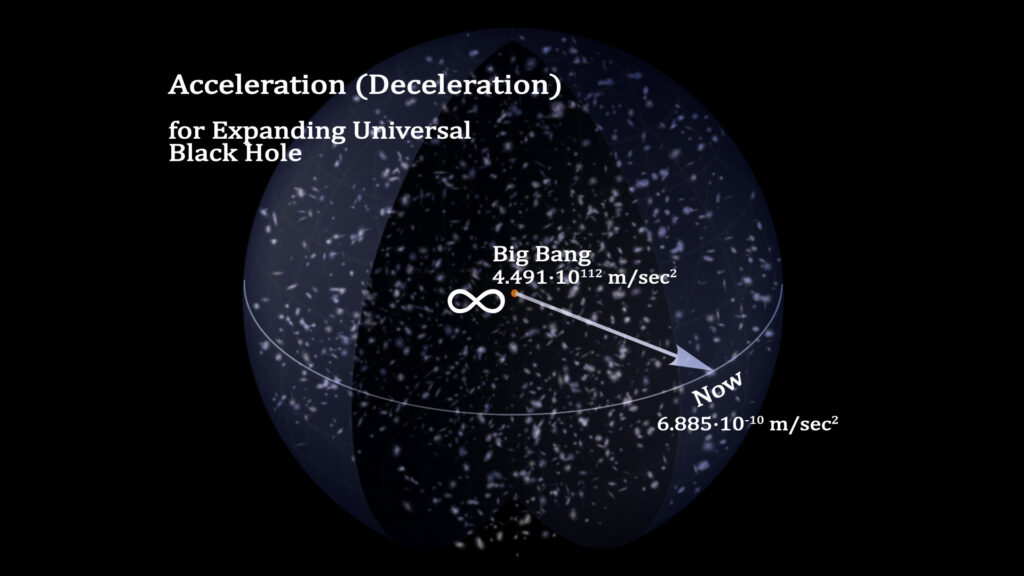
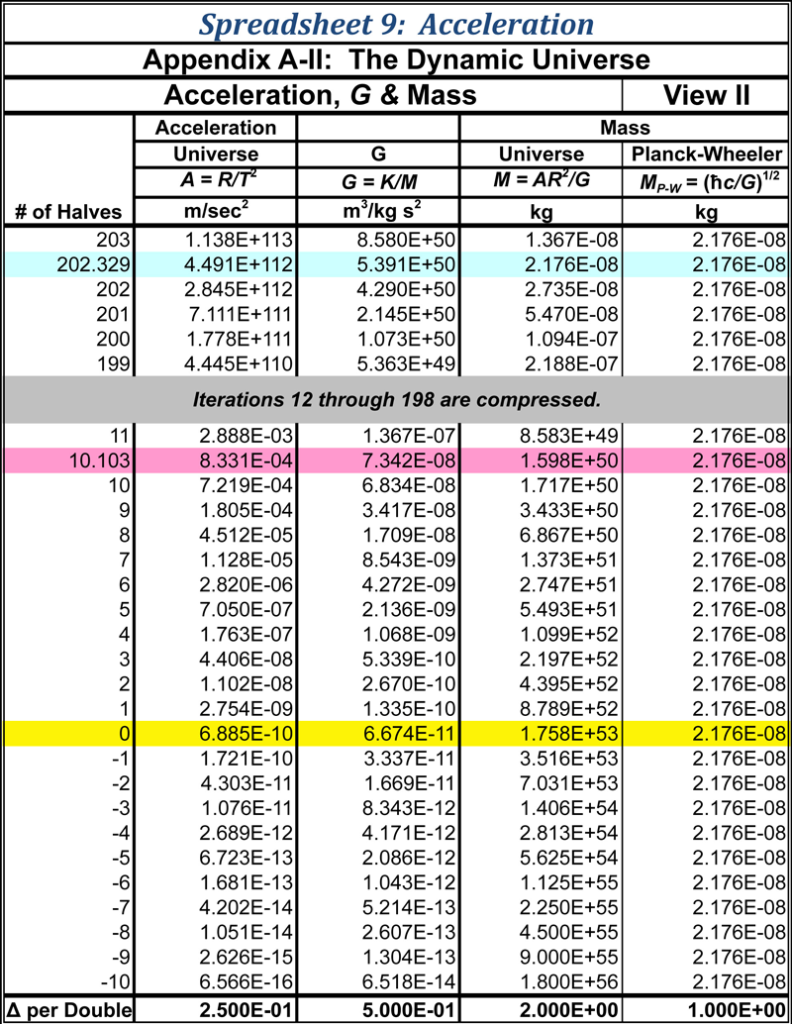
The time flow for a mass on the surface of the Universal Black Hole changes relative to the distance from the Universe’s center, i.e., the Big Bang. At the Big Bang the velocity of light was 8.520 • 1038 ms-1. This was the velocity of the expansion of the Universe. The Universe’s expansion slowed dramatically in the early phases of its formation. The acceleration rate (deceleration of the rate of expansion) at the Big Bang was 4.491 • 10112 ms-2.
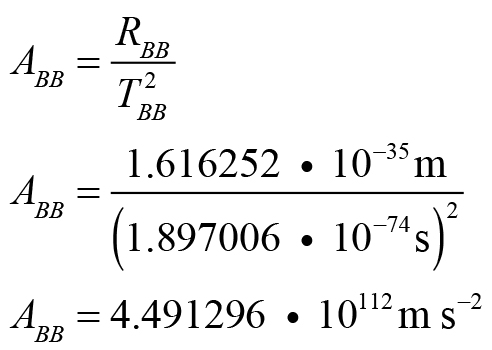
As the expansion proceeded, the acceleration rate of the Universe decreased to the present 6.885 • 10-10 ms-2.
Here is a place where the current paradigm for black holes varies significantly from Occam’s Razor. The existing theory establishes an acceleration that grows towards infinity as a mass falls to the theorized central singularity. This paradigm does not recognize that the event horizon for a black hole within this Universe experiences infinite acceleration at the horizon.
However, the reinterpretation of the General Relativity via the Schwarzschild metric describes a different structure for acceleration. The paradigm does accurately describe acceleration within the Universal Black Hole. A = R/R2 = 1/R is the identical formula for acceleration under the existing paradigm. The acceleration of a black hole Universe is the same as the accepted formulation for a black hole within this Universe.
But this acceleration differs in three crucial ways from the old Schwarzschild metric interpretation: 1) The central singularity of General Relativity is the Big Bang and not an infinitely dense junk heap of crushed mass. 2) Acceleration is not of an inward moving mass. It is a deceleration of the expansion itself. 3) As the Universal Black Hole decelerates the horizon’s expansion, the velocity of light, declines by a like amount so 1/R•c2 changes with light’s velocity.
Time flow decelerates towards zero as the event horizon is approached for a black hole within this Universe. For the Universe within, time flow accelerates with each incremental step away from the Big Bang center. The progenitor universe sacrifices its event creation for the Universe within.
So for black holes, it is a “tale for two accelerations”: One is for a black hole within this Universe’s spacetime containment. The other is that of a universe housed within the black hole where acceleration counters its rate of expansion and is based on the time flow created from that expansion.
The Accelerating Universe Illusion
In the late 1990s observations of type Ia supernovae led to a belief that the Universe was not slowing down under the effects of gravity. It was felt that the Universe was actually accelerating. Since then there have been several possible theories put forward to explain how the Universe could be accelerating.
One aspect of the Universal Black Hole theory is that the velocity of light has slowed with the rate of expansion. Ironically, a decrease in the velocity of light results in a shortening measuring stick. Distances in astronomy are measured in time-based units, i.e., light-year or light seconds. Since c has declined with the expansion, the measuring stick is becoming shorter. It takes light longer to travel between two astronomical objects than it did several billion years ago. The net effect is that the Universe is becoming less accessible.
When the Universe’s radius doubles from now, the velocity of light will decline to 1/√2. This will reduce the light year accordingly. The net effect is that the Universe will become increasingly inaccessible. Distant objects will seem even more remote than their calculated distance would indicate.
When on a shell near a massive astronomical object, time has slowed. The effect of slowed time is that wavelengths of light from distant objects are shortened as the apparent frequency increases. If the observer ignites her rockets and moves to a higher shell, she would find that the frequencies from the objects she had observed at the lower shell are slowed and that the light wavelengths have increased. The effect is these objects appear to have moved away from the observer and that the light distance has increased.
As time accelerates, so does apparent distance. This happens to the Universe . With passing time the Universe moves to higher radii, time accelerates, and apparent distances increase more than their “real” distance would indicate.
- Neutral energy refers to a mass beginning in flat spacetime that has no net movement towards or away from a large mass. It assumes that this mass becomes attracted to the larger mass and falls radially. The total energy of motion in this situation is equal to the rest mass of the object in flat spacetime. When the attracted mass coalesces with the black hole, it contributes its rest mass alone. No energy is added or subtracted due to an initial energy of motion relative to the black hole.
