Download this chapter for offline viewing (no videos, 5MB)
Download this chapter for offline viewing (includes video content, 130MB)
The Occam’s Razor approach to the description of the Universe has led to the Universal Black Hole solution. This model needs to be examined to determine if it has any credibility under the formulations of General Relativity. It should be pointed out that the current paradigm for black holes, and in particular the idea of a central singularity, requires reassessment.
Author’s note: This chapter is more complex than the others. It constitutes wrapping together the simplicity of Occam’s Razor into the elegant formulations of General Relativity. The reader can skip this chapter without sacrificing the essence of the overall presentation.
The Radius of Mass
Masses have radii of curvature such that if the mass is contained within that radius it will overwhelm the forces of matter and form a black hole. This curvature is defined by the Schwarzschild radius:
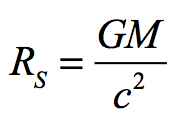
The formula is so imbedded into the language of science that relativists will often refer to a mass by its radius of curvature in meters rather than its mass in kilograms. The Earth’s mass is often referred to as 0.44 meters rather than 1024 kg, and the Sun has a mass of 1.5 kilometers.
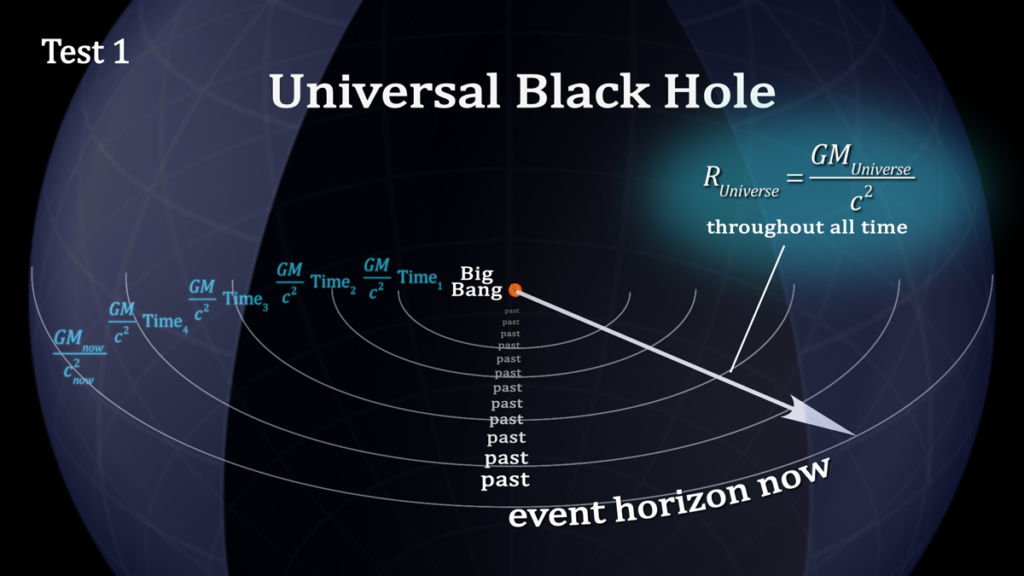
However, it is seldom if ever said that the Universe has a mass of 1026 meters, but this is in fact the case. The mass density of the Universe demands that the Universe form a black hole. Arguments that an expanding universe can’t be a black hole are not supportable. The present cosmological paradigm ignores the required Schwarzschild radius even though there is nothing in General Relativity that says this formula doesn’t apply to this or that special case. It is clear that the early Universe had the required density to form a black hole, but though less obvious in its current low density state, it is just as true today.
A consequence of the Universal Black Hole is that the Universe shares a common present. This present is determined by the required radius for the event horizon of a black hole. It is the transitional nature of the event horizon that unifies the four forces of physics.
The Schwarzschild Metric
Karl Schwarzschild in 1916 just months after Albert Einstein released his theory of General Relativity was able to simplify Einstein’s formulations to what has become known as Schwarzschild geometry. He developed his metric shortly before his death as a casualty of WWI. Following is his metric based upon the movement in spacetime within the curvature of gravity:

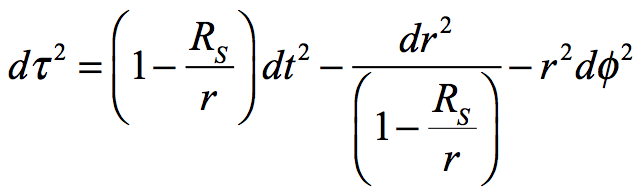
where:
| dτ | = (tau) local time passage of a mass |
| dr | = the change in radius |
| dt | = the change in time as measured by a distant observer |
| RS | = Schwarzschild critical curvature radius |
| r | = mass’s radius from gravitational center |
| dΦ | = change in angle relative to the center of gravity |

We use Γ to simplify the Schwarzschild equation in the same way that lower-case gamma (γ) is used in the metrics for Special Relativity:
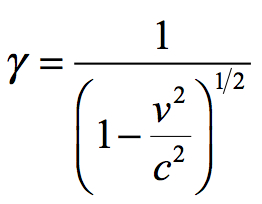
The Schwarzschild formulation determines the local movement of time (wristwatch time) in curved spacetime. The first factor relates position within the gravitational field to flat spacetime. The second factor tracks the change in the radial position relative to the center of gravity and the final factor tracks the change in tangential position.
Energy in Freefall
A mass possesses a rest energy equal to its rest mass times the velocity of light squared (E0 = m0c2). Mass in movement can be accreted by a black hole in an infinite number of pathways. Each pathway has its own unique energy (E) relative to the black hole. In one special case where the mass is dropped from a near infinite location1 with no initial net velocity towards the black hole, the total energy at all times during freefall will be equal to its initial rest energy E0.
For all other masses, the accretion energy will be E, which includes the initial energy of movement either towards the black hole or away from it. In this case E is equal to Special Relativity’s factor γ (gamma) with respect to the mass center of the black hole times its rest energy E0, such that E = γE0.
Energy is a conserved quantity. It always remains the same. When a mass moves into the curved spacetime of a black hole, it will always maintain a constant energy. The energy of a mass in freefall will be shown to have a conserved energy. If measured from a distance, this energy will convert from kinetic energy to potential gravitational energy, while when measured by an observer in a passing shell, it will be observed as kinetic energy. In all cases the combined rest and momentum energy will remain unchanged since energy is a constant of motion. The energy of a mass before accretion plus the mass of the black hole will equal the energy of the black hole after accretion. Mass and energy here are interchangeable.
Since E = mc2, E/mc2 = 1. Since c is a constant, it can be eliminated for simplicity. Energy can be stated in unitless terms, i.e., the ratio E/m to 1. However, the energy will be measured differently by observers with different clocks. The time of a distant observer with no net motion relative to the black hole is t. An observer’s time in the curvature of gravity is τ. The relationship between t and τ is:

Neutral Energy Freefall Velocity
If a neutral-energy mass freefalls towards a black hole, its energy of motion equals its rest energy (E0). Since there is no tangential movement in a neutral-energy freefall, the basic Schwarzschild metric can be converted to strictly radial movement. Assume a mass is in freefall in a gravitational field that has only radial movement, i.e. r2dΦ2 = 0. Reduce the formula to one that only includes radial motion:
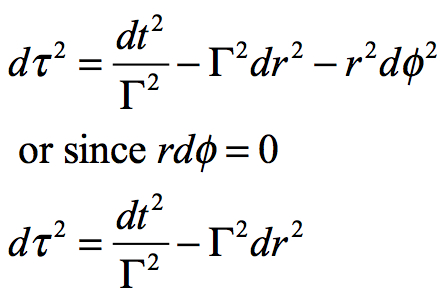
When this function and the function from the previous section are equated:
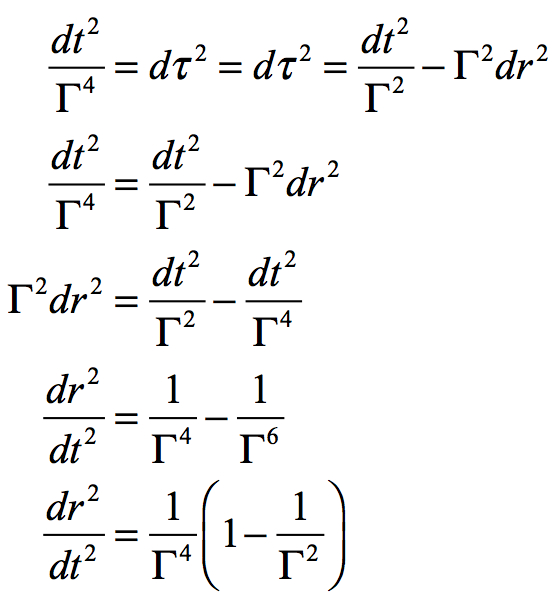
Convert Γ to its original components.
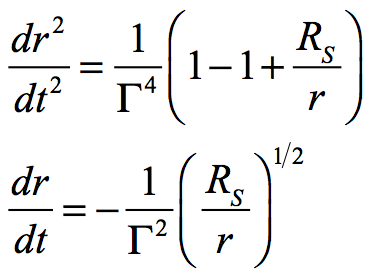
As r goes to RS, the freefall velocity will go to zero with respect to an observer who experiences time as dt at an infinite distance. To determine a velocity relative to that seen by an observer on a passing shell, this must be converted to shell spacetime (drshell/dtshell). From manipulation of the basic Schwarzschild metric:
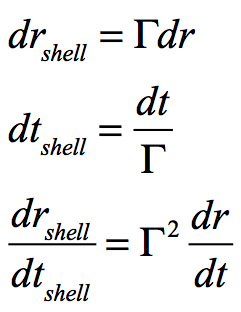
since:
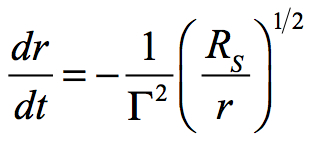
then:
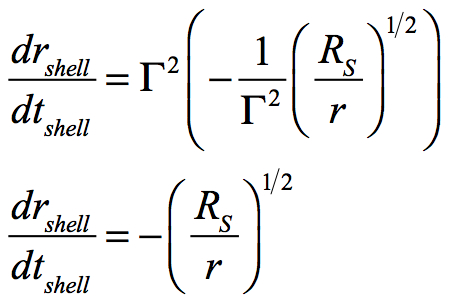
A shell observer of a passing freefall mass will observe the same velocity, i.e., β = – (RS/r)1/2 as the freefall mass observes while passing the shell observer, but the time flows vary considerably between the two divergent vantage points.2
Velocity of Freefall at the Event Horizon
A consequence of the neutral-energy freefall is that at the unique radius where r = RS the velocity of freefall equals that of light or c:

The infall velocity is mandated to be that of light at the event horizon. The event horizon has a locally measured required infall velocity c, but time at the event horizon relative to a distant observer is zero so inward velocity of a mass at the horizon as seen from an observer at a higher shell, is zero. This leads to the dual nature of black holes.
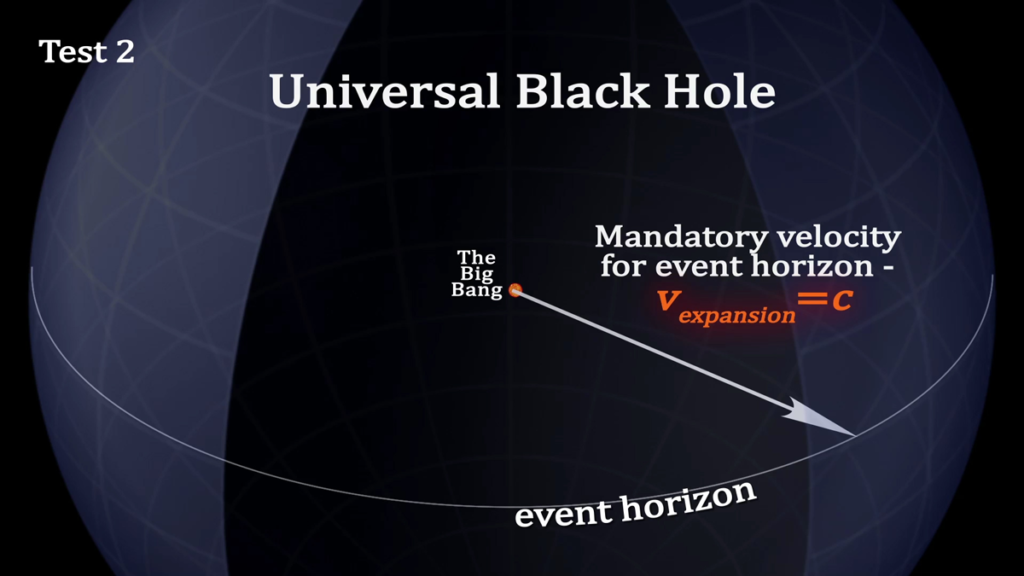
The event horizon for the universe within represents an entirely different perspective. The horizon velocity for the Universal Black Hole is mandated to be c. Therefore, the Universe expands at the velocity of light as dictated by General Relativity.

Direction of Freefall Past the Event Horizon
A consequence of Schwarzschild’s metric is that for freefall past the horizon of a black hole the components of the metric reverse signs, i.e., when r < RS. This can be seen if we return the Schwarzschild metric back to its original components, i.e.,
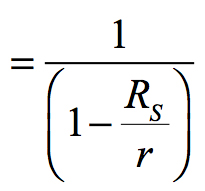
Beyond the event horizon
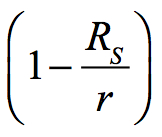
becomes negative when r < RS. Therefore:
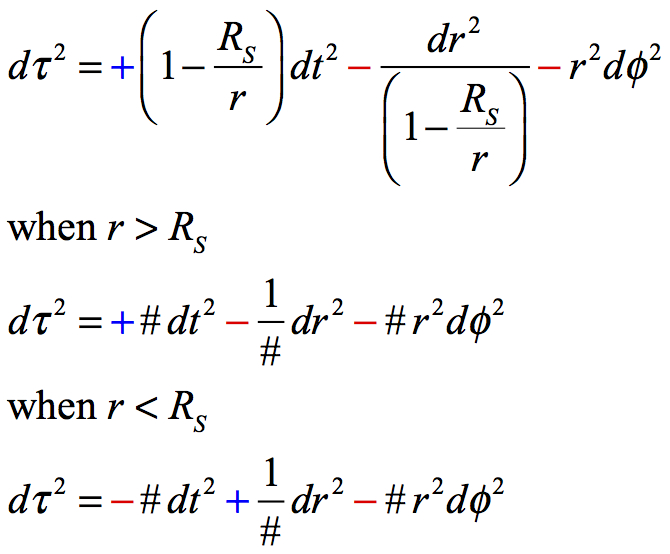
In essence the signs reverse for the movement in time and the movement in space once a mass has fallen beyond the event horizon. This means that the direction of movement and the direction of time reverse inside the event horizon of a black hole. What is being introduced here is that the Universe is a black hole. The formulations for radii within the black hole are those for our Universe when it was at a younger age.
While the direction of movement for a black hole is inward until the horizon is reached, inside of the horizon the direction of spacetime is outward. Just as black holes grow when mass is added, the Universe grows as its mass increases. With this growth, the Universe expands.
In Exploring Black Holes – Introduction to General Relativity, by Edwin F. Taylor & John Archibald Wheeler the following quote describes the nature of spacetime inside the black hole according to the current paradigm:
“Inside there is an interchange of the character of the t-coordinate and the r-coordinate. For an r-coordinate less than the Schwarzschild radius RS3 the curvature factor (1 – RS/r) in the Schwarzschild metric becomes negative. In consequence, the signs reverse between the radial part and the time part of this metric, making the dt2 term negative and the dr2 term positive. Space and time themselves do not interchange roles. Coordinates do. The t-coordinate changes in character from a time-like coordinate to a space-like coordinate. Similarly, the r-coordinate changes in character from a space-like coordinate to a time-like one.
What does it mean to say that inside the Schwarzschild radius the r-coordinate ‘changes in character from a space-like coordinate to a time-like one?’ It means that our free-float frame moves to ever-smaller r with all the inevitability that we ordinarily associate with the passage of time. The explorer in his jet-powered spaceship prior to arrival at r = RS always has the option to turn on his jets and change his motion from decreasing r (infall) to increasing r (escape). Quite the contrary is the situation once he has allowed himself to fall inside r = RS. Then the further decrease of r represents the passage of time. No command the traveler can give to his jet engine will turn back time. That unseen power of the world that drags everyone forward willy-nilly from age twenty to forty and from forty to eighty also drags the rocket in from the coordinate r = RS to the later value of the ‘time’ coordinate r = 0. No human act of will, no engine, no rocket, no force can make time stand still. As surely as cells die, as surely as the traveler’s watch ticks away the unforgiving minutes, with equal certainty r drops from RS to 0 with never a halt along the way.”4
Taylor and Wheeler do not accept that the movement within the horizon of the black hole is outward since intuition fights against what the Schwarzschild metric actually states. The reversal of the sign of the r-coordinate to positive actually means the reversal in the direction of radial movement.
However, the quote is talking about radial movement as being timelike. In the Universal Black Hole model the inevitability of radial movement is not only timelike, it is the movement of time. The radius of the Universe increases with time. All mass must follow the expansion in lock-step with the movement of time. The Universal Black Hole model is the true manifestation of the formulations within the Schwarzschild metric. Black holes expand outward. Radial movement is time, while tangential movement becomes the movement in space.
These differences can be attributed to the literal interpretation of the Schwarzschild formulations. The importance of the conclusions here cannot be overstated.
Velocity of Freefall Past the Horizon
If the neutral energy freefall velocity is equal to

– then what is the velocity relative to c when r < RS? Since the numerator is larger than the denominator, this ratio becomes greater than one. The ratio is β (beta). (Here β is the percentage of the velocity of light.) A β greater than one means that the freefall velocity exceeds that of light. This is apparently a violation of Special Relativity.
The velocity of light is the rate that space and time are created by the expanding Universe. This rate is determined by the proportionate radius of the Universe. While the current velocity of light is 2.99792458 • 108 ms-1, its velocity in the past varied according to General Relativity’s formula
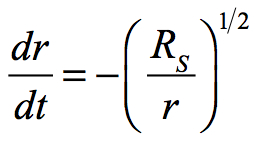
for the change in radius. The neutral-energy formula needs to be revised for the Universal Black Hole. The General Relativity formula changes as follows for the Universe:
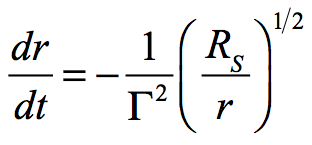
The formula changes as the direction of freefall is now outward. This has the effect of changing the sign of the exponent to – 1/2 from + 1/2. Instead of moving to lower radii, masses move towards higher radii and a decreased velocity of expansion.
The current paradigm for black holes accepts a freefall exceeding c on a mass’ journey to the central singularity. It is argued that even though the required velocity of freefall exceeds c, there is no stable shell vantage point from which to observe the excess velocity because all of spacetime is falling towards singularity at the same velocity.
The Universal Black Hole theory changes the entire picture. Freefall is now outward. Radii less than the event horizon are past event horizons when the Universe was at a younger age. The free-fall velocities inside the current radius of the Universe remain embedded in the formulas for General Relativity, but these are the velocities for the movement of spacetime in the past. This movement is stated in terms relative to that velocity today. At no point does mass move at greater than c. The inside of the black hole is just past horizons. Each past horizon had a mandatory spacetime velocity of c. It’s just that light’s velocities then were higher than today. This is in keeping with General Relativity’s and with Keplerian spacetime.
Time Passage Beyond the Horizon
Freefall outside of the horizon can vary depending upon the angular momentum, the total energy of the mass relative to its rest energy, or whether there are rocket engines to slow the change in velocity, but inside the event horizon the radial movement is mandatory. Each radius has a required velocity relative to that of light. Therefore, the radial movement within a black hole is always absolute. We have come to know this absolute movement as time.
The Schwarzschild metric determines the rate of infall for the current paradigm. However, the Universe does not freefall towards singularity; it expands outward from the Big Bang singularity. The new paradigm for the nature of black holes establishes that inward movement is negative time. This means that outward movement is positive time. Nevertheless, the formulations for General Relativity’s rate of freefall within a black hole apply to the outward moving Universal Black Hole.
The t-coordinate inside of the horizon becomes the flow of time for the black hole’s separate and distinct system of thermodynamics. The mandated rate of the now positive freefall vector becomes the rate of movement for spacetime for the black hole’s system of thermodynamics. The velocity of light would then vary depending upon the changing radius of the black hole.
If Rhorizon is the radius of the Universe now or Rnow and r is the radius of the Universe in the past or Rthen, then the velocity of light of the past relative to now would be:
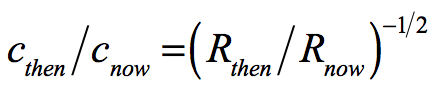
What if the age of the Universe were to be the freefall time under General Relativity? Then the time relationship between the present and the prior point in the Universe’s history would be determined by the integration of the rate of freefall. This formulation as adapted from Taylor & Wheeler’s Exploring Black Holes; Introduction to General Relativity, page B-6 would be:
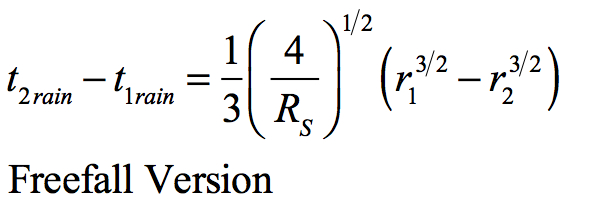
(Note that time changes to the 3/2s power of the proportional Radius.)
In this formula t2rain resides at a lower radius within the black hole than t1rain since the current paradigm for black holes mandates that movement is always inward towards a central singularity. While the author disagrees with this viewpoint, the formula effectively identifies the difference in time for radial movement between two events. For the Universal Black Hole it has already been shown that the new interpretation for the direction of movement inside the event horizon of a black hole is outward. Therefore, Tnow and Tthen are reversed from the formula above where t2 resides at a lower radius than t1. Here now is at a higher radius than then.

Universe Velocity
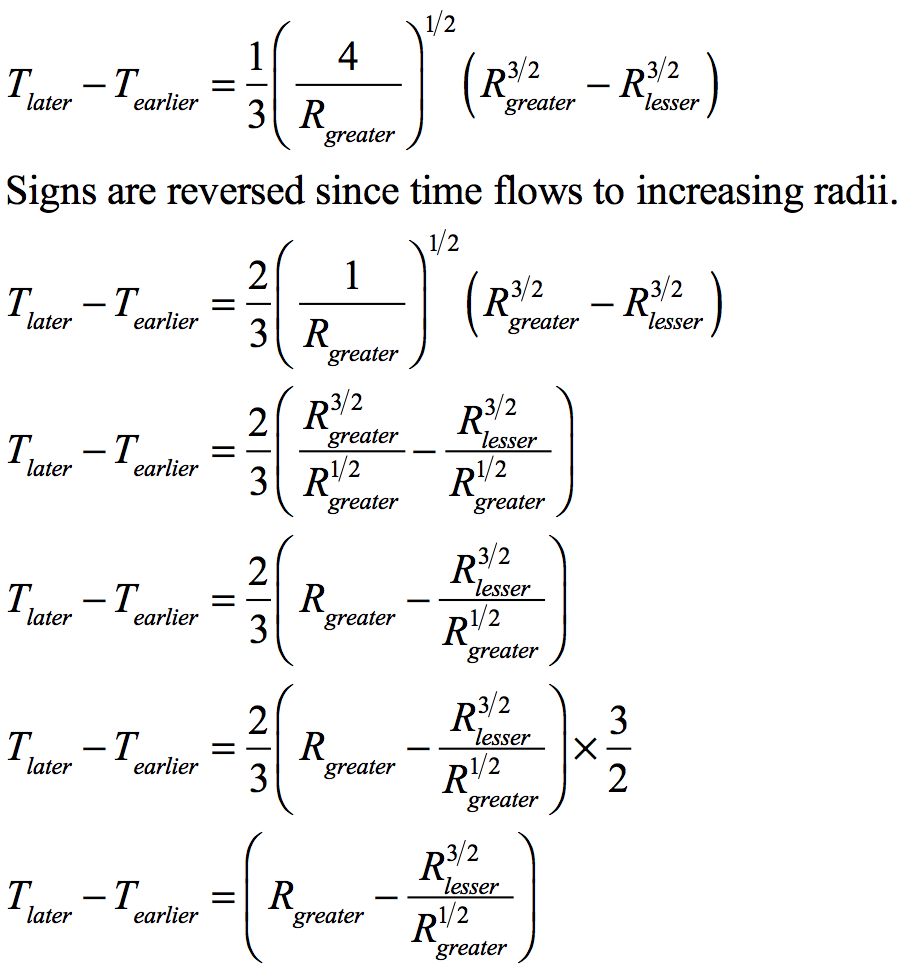
The 3/2 adjustment factor is necessary to account for the fact that a black hole is different when viewed from within than from without. Under the current paradigm the time that it takes to fall from the event horizon to the central singularity of the black hole is 2/3 the time that as it would for light to travel the radial distance in flat spacetime. Since time within the Universal Black Hole is a product of its internal physics, the age of the Universe for its current event horizon is unitary. Therefore, the 2/3 factor must be offset by multiplying by 3/2 to make the time that it took for the Universe to expand to the current radius equal to the age of the Universe.
If we replace Tlater by Tnow, Tearlier by Tthen and Rgreater by Rnow, Rlesser by Rthen, the formula becomes:

Under General Relativity freefall beyond the event horizon results in greater velocities towards the center of the black hole than near the event horizon. The freefall time between different radii is based on a ratio of the two radii to the 3/2 power. This shows that time changes in like proportion. General Relativity confirms the relationship of time to radius for the Universal Black Hole.



Summary
- Test 1: The radius of the Universe is that of a black hole with the Universe’s current mass.
- Test 2: The velocity of expansion is the velocity of light, which is the mandatory velocity for the event horizon of a black hole.
- Test 3: The inversion of the sign for the r-coordinate and the t-coordinate of the Schwarzschild metric establishes that the movement of spacetime within the event horizon is outward. This is the case with the expanding Universal Black Hole.
- Test 4: The freefall velocity for the Universe’s gravitational system is the velocity of light. This is the movement of spacetime for the expanding Universe. The velocity of light has changed over the history of the Universe according to the mandatory radius-dependent velocity inside the black hole.

- Test 5: The freefall time between different radii for black holes varies to the 3/2 power with radius in the same way that the Universe ages.

Conclusion: The Universal Black Hole is not just a possible option. It is the required solution to the equations of General Relativity.

- An infinite location would produce no net attraction to the black hole. The special case here refers to movement of a minor mass with the exact escape velocity from a black hole but with a reverse vector towards the black hole.
- β equals the velocity relative to that of light.
- RS is substitute for 2M in the quote.
- The fundamental difference between the current paradigm and the one expounded here is that the point of action for a black hole is the event horizon and not a central singularity. The author has made the small adjustments to existing formulations to account for the difference.
