Download this chapter for offline viewing (no videos, 1MB)
Download this chapter for offline viewing (includes video content, 14MB)
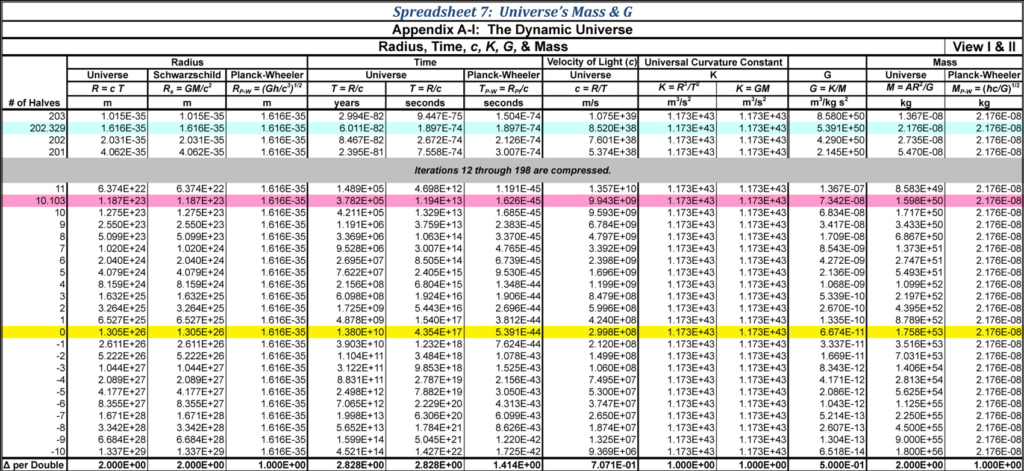
The Universal Black Hole began at Planck-Wheeler’s mass and a curvature that had a Planck-Wheeler radius. Since that first moment in time, the mass of the Universe has increased causing the radius of the Universe’s black hole to increase linearly. As the mass of the Universe has increased, the gravitational factor G has decreased in like proportion to account for the smoother curvature of space and time such that GM has always remained equal to the constant K.
Packing All of this Stuff into the Big Bang
The question is: “Can mass be either created or destroyed?” In other words, is the mass in the Universe today the same as at the Big Bang? Can all of the matter and energy that we know in the countless billions of stars in countless billions of galaxies be compressed into the incredibly tiny space of the Big Bang?
Clearly it doesn’t make any sense that all of this stuff could fit into such a tiny confinement. Compressing 1053 kg to 10-35 meters creates a black hole equal to the size of the current Universe assuming the G and c were the current values. The Universe becomes nonsensical.
The only value for the Universe’s mass that makes sense is Planck-Wheeler’s mass. As the Universe expanded this initial mass increased linearly with radius just as the Schwarzschild metric mandates:
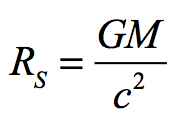
Radius increases directly with mass just as it does with black holes in this Universe. Previously, we looked at the Schwarzschild radius for Earth and came up with 0.88 cm. Whereas, the Sun is 333,000 times the mass of Earth and consequently has a critical black hole radius of 3 kilometers.
G
The units for Newton’s Gravitational curvature factor are:
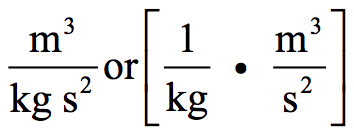
Included in G is the Kepler-Otto Universal Curvature Constant (K):

The element that remains is the inverse of mass (kg-1). Since K = GM, then:
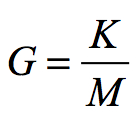
Therefore, since K is always constant, as M increases with radius, G decreases proportionately. Simply dividing the constant K by the Universe’s mass determines a value for G.
Derivation of G at the Big Bang
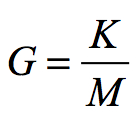
and since K has always been a constant, the value of G at the Big Bang can be calculated. M and G behave as reciprocals to each other. We now know the mass of the Universe today and also the mass of the Universe at the Big Bang. With these quantities, we can calculate G at the Big Bang.
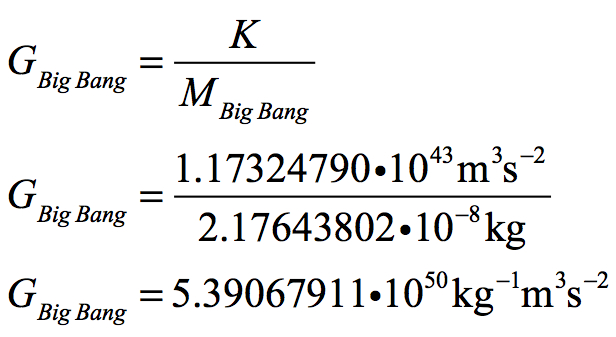


GM
When G and M are multiplied, they create a constant that has been unchanged throughout the Universe’s history. G at the Big Bang was 61 orders of magnitude greater than today. This is a result of the high curvature of the Universal Black Hole at the Universe’s formation.



Gravity and Spacetime Curvature
All mass resides on the surface of the Universal Black Hole. This surface is the event horizon. There is a curvature to the surface. As events move from the present into the past they move from the horizon surface into the interior of the Universal Black Hole.
Mass takes up a discrete surface area on the Universal Black Hole’s horizon. The greater the mass, the greater the occupied surface.
The black hole surface has a curvature. As events move from the present into the past, they move from a flat two-dimensional surface to one with the curvature of the contained space in the past. This spatial transition leads to Einstein’s spacetime curvature.
When the Universal Black Hole was small in its beginning, the curvature transition was quite large. Just as small black holes have a greater tidal effects, so does a smaller black hole Universe have a greater G curvature. As the mass of the Universe increased, so did the surface area of the Universal Black Hole. This produced a surface with less curvature per unit of surface mass and consequently a lower G.