Download this chapter for offline viewing (no videos, 2MB)
Download this chapter for offline viewing (includes video content, 18MB)
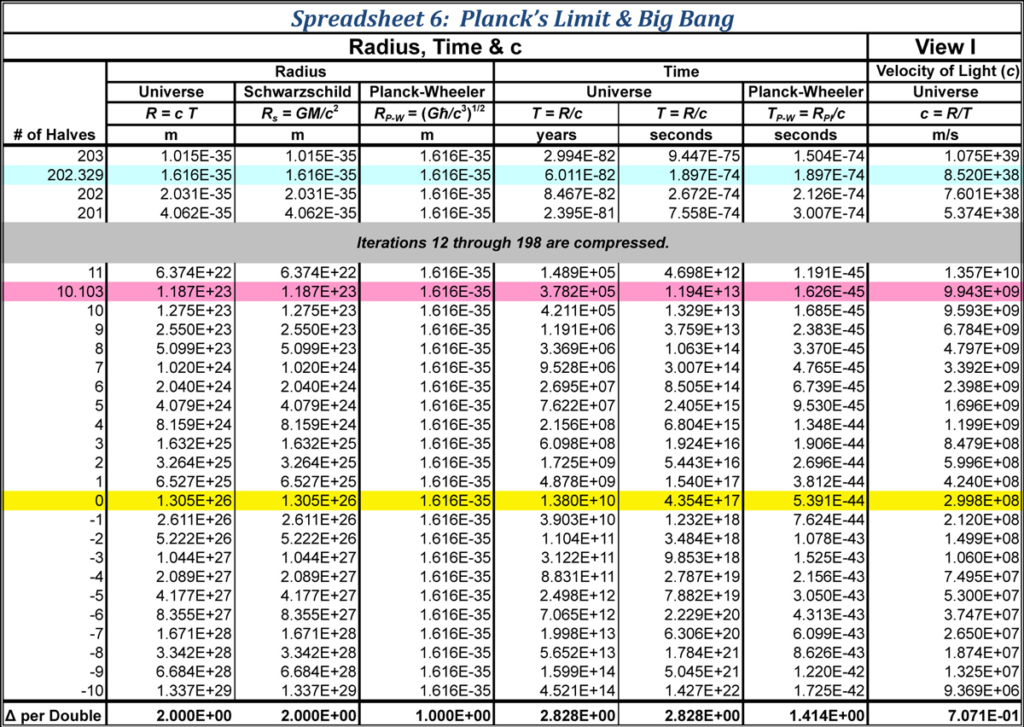
An effective technique to understand the early Universe is to reduce the radius in 1/2 multiples until Planck’s distance is reached. After 202.329469427 iterations the Universe’s radius reaches Planck’s length. It is here that Planck’s length, the shortest possible wavelength, matches the Schwarzschild limit of the Universal Black Hole and the Big Bang is revealed.
The Merger of Quantum Mechanics and General Relativity
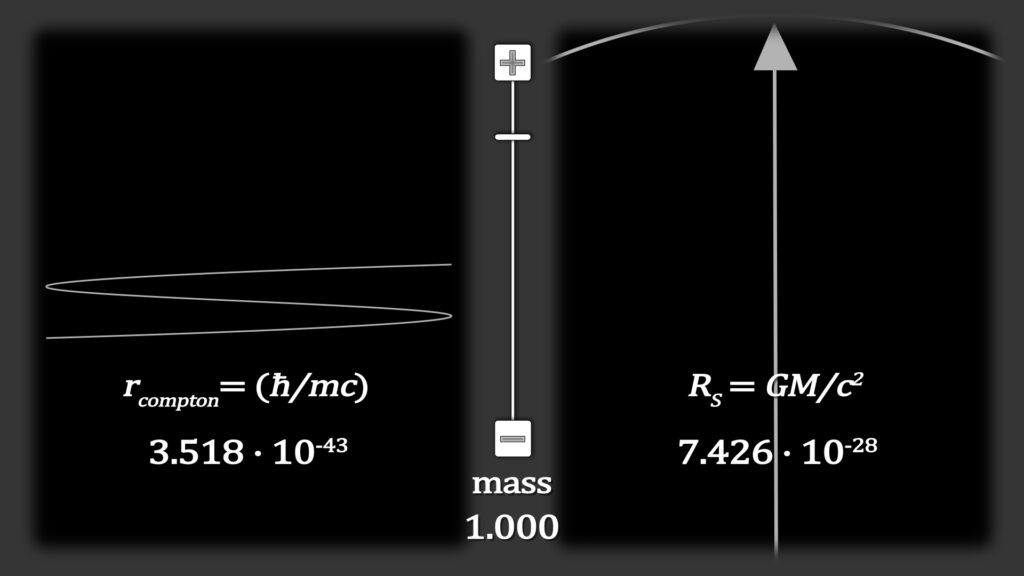
Quantum mechanics and General Relativity come together naturally at a unique distance known as the Planck-Wheeler Radius. Louis deBroglie determined that just like light all matter has waveforms. Matter and energy are interchangeable according to Einstein’s formulation E = mc2. Arthur Compton determined the formula for the wavelength of light that was necessary to equal the total energy of a particle if the entire mass of an object were to be converted to electromagnetic radiation. The resulting wavelength of the light would be the Compton wavelength of that mass. The radius of that wavelength is determined by dividing Planck’s angular momentum factor ħ by the mass of the particle times the velocity of light:
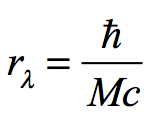
This is the pushing out force of quantum mechanics. Note that the greater the mass, the shorter the wavelength. In contrast, mass constrains spacetime into a black hole according to the formula:
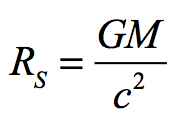
Note that the two radii are inversely related to mass. The larger the mass, the greater is the radius of gravitational curvature, but the larger the mass, the shorter is the rest-mass wavelength. This raises the question of: for what mass are the radiuses RS and rλ equal?
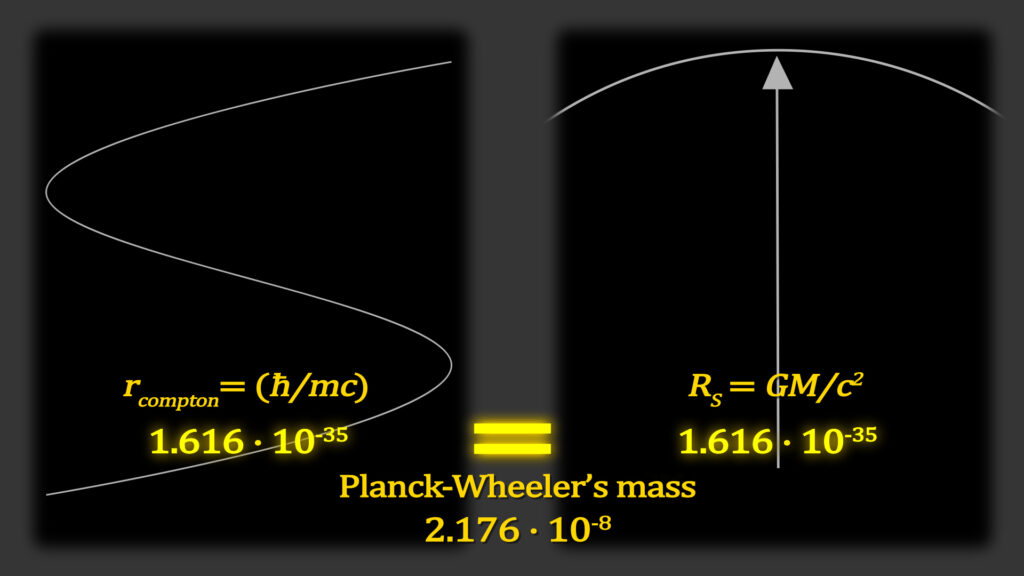
If we take the wavelength equation and the gravitational curvature equation and equate the two radii, we can reveal the formula for calculating Planck-Wheeler’s mass.
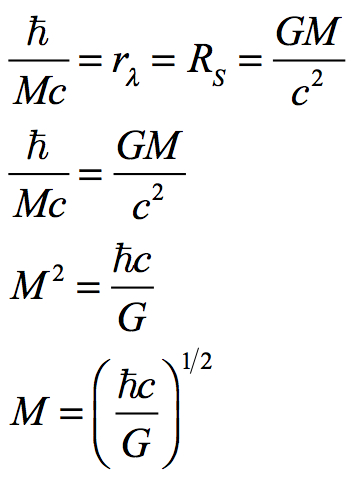
Since this is an extremum that is a product of Planck’s angular momentum, we refer to this mass as Planck-Wheeler’s mass. Therefore:
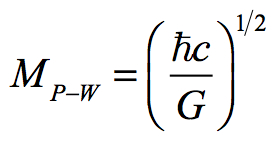
Since all of the factors in the equation are known for the current Universe, we can solve this equation and calculate MP-W:
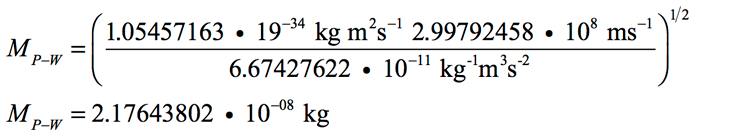
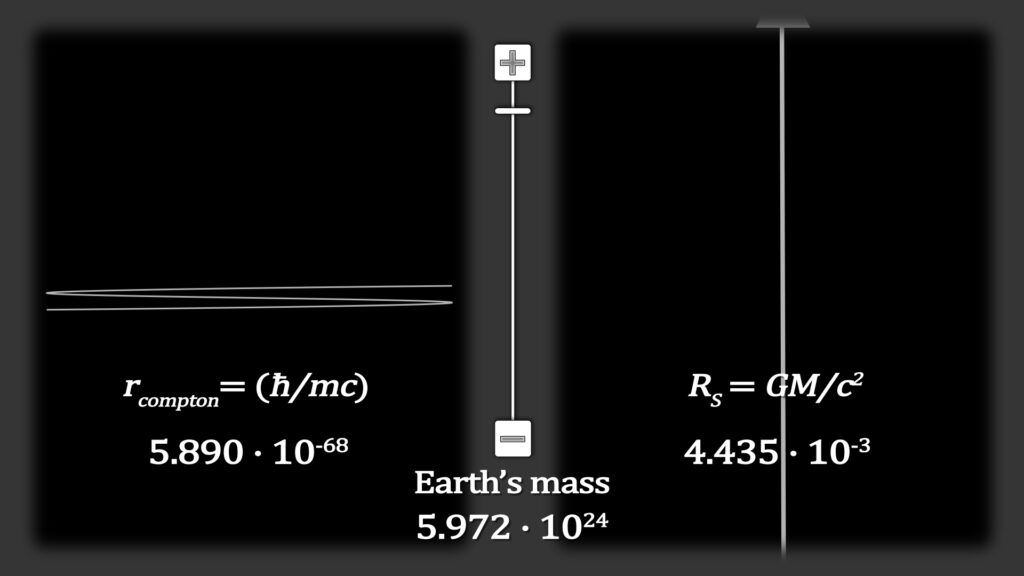
The cross-over mass is shown in the following illustrations. Note that large masses produce larger Planck-Wheeler radii, while at the same time they produce shorter Compton waveforms. In contrast for smaller masses the opposite can be said. At Planck-Wheeler’s mass the two radii merge.
We refer to this quantity as Planck-Wheeler’s mass since it is an extremum quantity as is Max Planck’s original Planck constant, which is the angular momentum of a single waveform. John Wheeler’s name became associated with this and several other extrema quantities by Kip Thorne in deference to the work done by his mentor. It is helpful here since there are other extrema quantities that need to be differentiated.
Planck-Wheeler’s Mass at the Big Bang
The formula for Planck-Wheeler’s mass should work for all phases of the Universe. By looking at the components of the formula and how they have changed over the history of the Universe, it can be determined what this quantity was at the Big Bang.
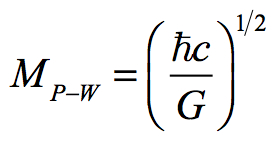
What has been determined is that c has changed to the -1/2 power since the Big Bang. G has been shown to have changed inversely with radius, i.e., to the -1 power. Planck’s angular momentum changed also. Angular momentum is based upon a mass, a radius and a velocity. As the velocity of light declines, so does angular momentum. ħ declines in step with the velocity of light, i.e., -1/2 power with radius.
So if both ħ and c declined by -1/2 power and if G declined by -1 power, then the MP-W would remain unchanged throughout the history of the Universe.
Planck-Wheeler’s Radius at the Big Bang
Until now it has been assumed that the shortest radius possible and therefore the radius of the Universal Black Hole at the Big Bang was Planck-Wheeler’s radius. Now using Planck-Wheeler’s mass this radius can be calculated. From above it has been shown that equating the radius of curvature for a black hole and Compton’s radius formula produces a unifying mass, which we call Planck-Wheeler’s mass:
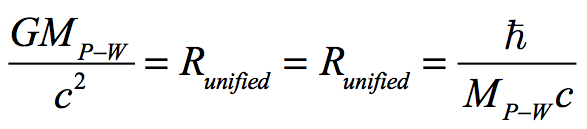
From this double equation the terms can be regrouped to calculate the unified radius by taking each equation and making them equal to one. When equated to one, one side can be inverted so that Runified will not be self-canceled:
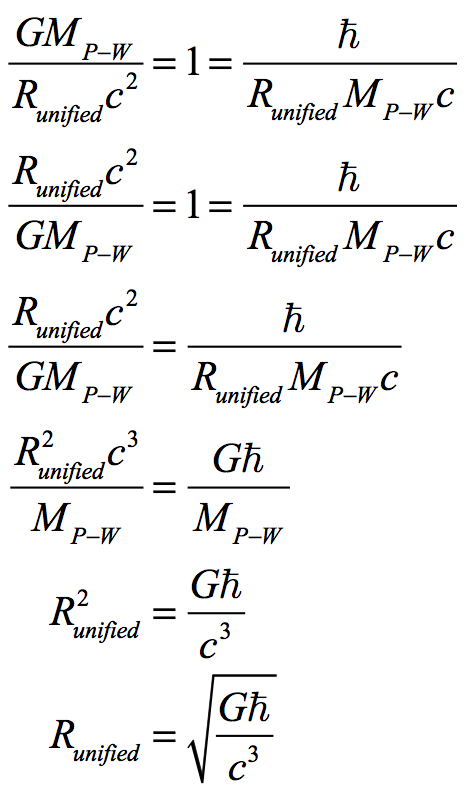
If we insert the calculated quantities for each factor at the Big Bang, we have:

The interesting aspect of this equation is that no matter what phase the Universe is in this equation yields the exact same result, i.e., when c was 1038 ms-1 at the Big Bang or 108 ms-1 now. The gravitational curvature factor times Planck’s angular momentum exactly parallels the change in c3.
As a consequence, Planck-Wheeler’s distance is a true constant for the Universe. There are major implications to this. Distance has an absolute aspect about it that time does not. This becomes apparent in the discussion of Planck-Wheeler’s time below.
Planck-Wheeler’s Time
Planck-Wheeler’s time is the amount of time that it takes light to traverse the shortest waveform distance, i.e., Planck-Wheeler’s radius.
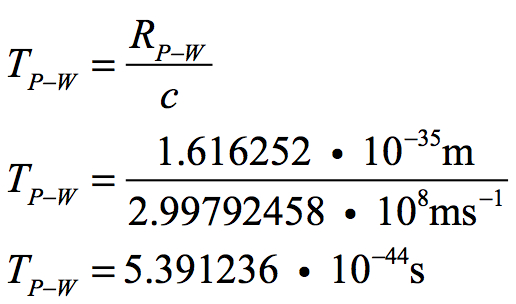
Since the velocity of light changes to the -1/2 power with radius and since Planck’s distance has always been the same as it is now, then Planck-Wheeler’s time changes to the 1/2 power with the increase in the Universe’s radius.
Reducing the Universe by Half Multiple Iterations
Up to this point the following quantities for the Universe have been determined for the present moment in the Universe: Radius, Age, Velocity of Light, Universe’s Mass, Kepler-Otto Universal Curvature Constant, Universe’s Density, Planck-Wheeler Mass, Planck-Wheeler Length, and Planck-Wheeler’s Time. In order to understand how the Universe has expanded since the Big Bang, we begin with the current values for these quantities and go backwards in time toward the Big Bang.
This can be done by reducing the Universe’s radius by 1/2 intervals repeatedly until we reach Planck’s length. Each of these quantities varies in a specific ratio relative to the 1/2 changes in the Universe’s Radius. In the chart below are those proportional relationships:
| Universe’s Factor | Proportion Relative to Radius |
| Radius (R) | ~R1 |
| Age (T) | ~R3/2 |
| Velocity of Light | ~R-1/2 |
| Mass (M) | ~R1 |
| Kepler-Otto Universal Curvature Constant | ~R0 |
| Universe’s Density | ~R-2 |
| Planck-Wheeler Mass | ~R0 |
| Planck-Wheeler Length | ~R0 |
| Planck-Wheeler Time | ~R1/2 |
If time is reversed and the Radius of the Universe is reduced in half, the age of the Universe will be (1/2)3/2 or 35.36% the current age. The velocity of light would be √2 its present value. Mass changes one for one with radius. Note that the radius of a black hole changes linearly with the change in mass. This is the case for the Universe’s radius.
Proportional Changes in the Various Universal Factor Quantities
When the radius of the Universe is reduced by 1/2 for 202+ iterations (actually 202.329469427), the radius of the resulting sphere is equal to Planck-Wheeler’s radius. The total change in the radius was sixty orders of magnitude:
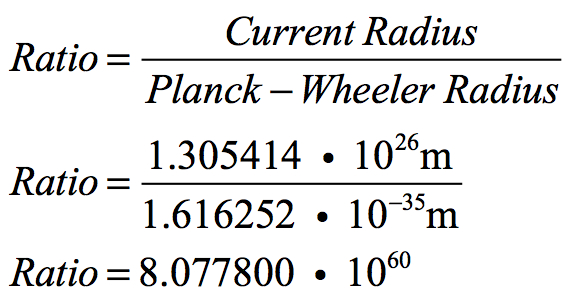
These other factors vary in a defined proportionate way to the change in the Universe’s radius. The relative change for each relative to Radius had been shown above. Each factor has changed, or in some cases not changed, accordingly since the Big Bang. That change in the value of these factors is indicated in the chart below.
The proportional relationships relative to Radius of each of these and future factors are explored here later. From these relationships the simple underlying structure of Occam’s Razor become apparent.
| Universe’s Factor | Change Since the Big Bang |
| Radius (R) | 1061 |
| Age (T) | 1091 |
| Velocity of Light | 10-31 |
| Mass (M) | 1061 |
| Kepler-Otto Universal Curvature Constant | 100 |
| Universe’s Density | 10-122 |
| Planck-Wheeler Mass | 100 |
| Planck-Wheeler Length | 100 |
| Planck-Wheeler Time | 1030 |
Conditions for a Universe
A universe requires two primary conditions: 1) It must exist as an independent entity, and 2) it must be able to recognize its own existence. What makes the Universe independent is the containment of its experience. Experience means that there must by a perceiving aspect to the Universe. Perception requires something to be perceived.
Those somethings are events. Events are generated by exchanges. Exchanges are between mass and energy. Mass observes and energy is that which is observed. Waveforms are the product of those exchanges.
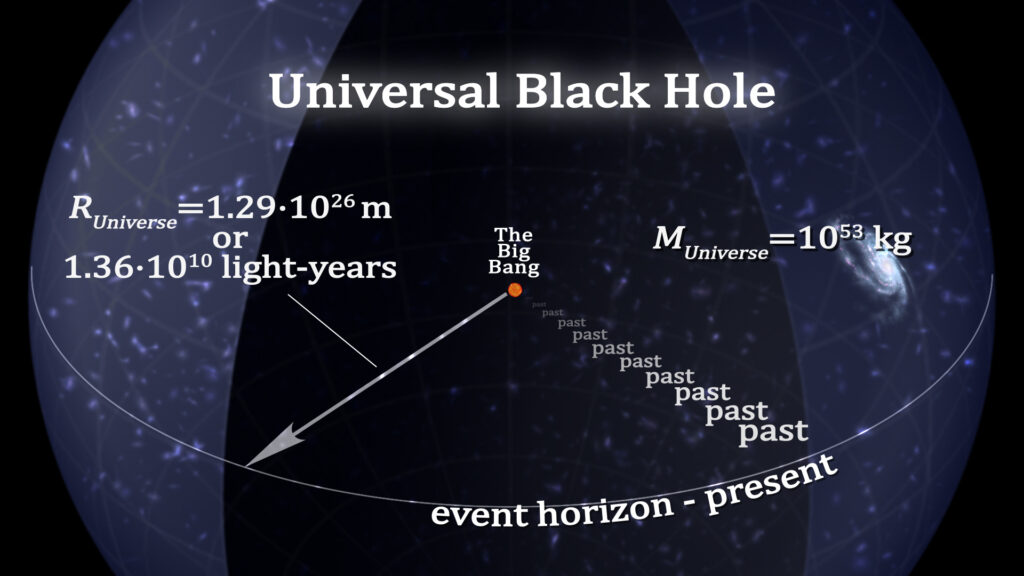
These two primary conditions must be in place for the Universe to exist. A universe with no boundary is an amorphous infinity. To even call it a universe, it must be identifiable as a single unit. By saying universe we establish finite. One can say this is one universe. One is finite. That one is provided by the closure inherent in the Universal Black Hole.
That universe may have infinite qualities, but by saying universe, those qualities have been reduced to the specific universal unit. Gravitational curvature has carved a universe from the endless character of infinity. This curvature is based in the nature of the Universal Black Hole.
The waveform accomplishes the second primary condition. It is the mechanism whereby a universe observes itself and with those experiences, generates the observing entity. By moving away from an experience a prescribed minimum radius the observing mass can utilize the laws of physics to observe the experiences of the past and in the process generate more experiences to be observed. The minimum distance that must be achieved is that unique number for our Universe that we refer to as Planck’s radius.
Mass develops from accumulated exchanges. The total accumulation of events resides in the Universe’s mass, and that mass resides on the surface of the Universal Black Hole.
The Big Bang Revealed
The first waveform for this Universe is the Big Bang. Its wave radius is Planck’s distance. Its observation is the space generated by its waveform. Its containment is the curvature of the procreating black hole. Its mass is the Planck-Wheeler mass identified here.
Planck-Wheeler’s mass is the unification mass for the quantum mechanical mechanism and the single waveform embedded in the Big Bang. It is also the mass necessary to generate an event horizon of an equal radius from which to observe itself.
It is fascinating that these simple formulations can reveal this epoch moment. With it comes not only existence, but the mechanisms, once set into motion, to generate all that we have come to know as the Universe. Many of these mechanisms for existence will continue to be explored here.