Download this chapter for offline viewing (no videos, 3MB)
Download this chapter for offline viewing (includes video content, 38MB)
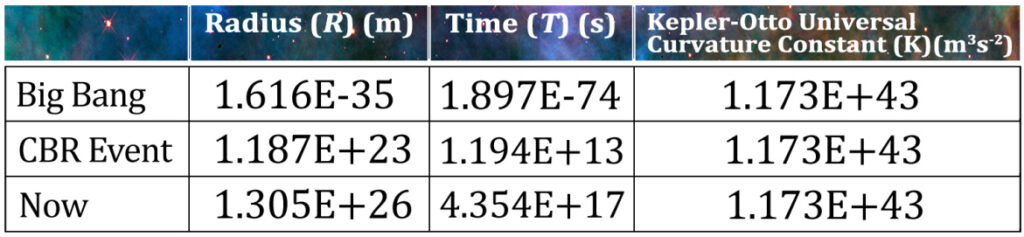
Johannes Kepler established that the relationship between the cube of a planetary radius and the square of its orbital period is a constant for the solar system. The same principles apply to the entire Universe such that the cube of the Universe’s radius divided by the square of its age is a constant. We can name this constant the Kepler-Otto Universal Curvature Constant (K). Unlike other mass-based systems, the spacetime curvature for the Universe’s gravitational system also determines G (Newton’s gravitational “factor”1) such that when the Universe’s mass (M) is multiplied by the gravitational factor (G), it also equals K.
Summary
It is time to review what has been established up to this point. In the first four chapters the radius, age, and velocity of light were all discussed. Chapter four provided a solution for the mass and mass density of the Universe.
Two physical concepts provided all of the solutions given here. They were: 1) the spacetime relationship derived by Johanne Kepler 400+ years ago, and 2) the Einstein-Schwarzschild solution for the radius of a black hole. In this chapter these two concepts will be unified into one based on the nature of the Universal Black Hole.
Keplerian Spacetime for the Solar System
Johannes Kepler established three laws of planetary motion. The first law stated that the orbit of a planet is an ellipse with the Sun located at one of the two foci. An ellipse can be formed by bisecting a cone with a plane. The steeper the plane relative to the vertical axis of the cone, the greater the eccentricity. When the bisecting plane is parallel to the base of the cone a circle is formed.

Kepler’s second law of planetary motion states that over any two equal time periods an orbiting body traces out equal angular areas between the orbiting arc and the central gravitational force.
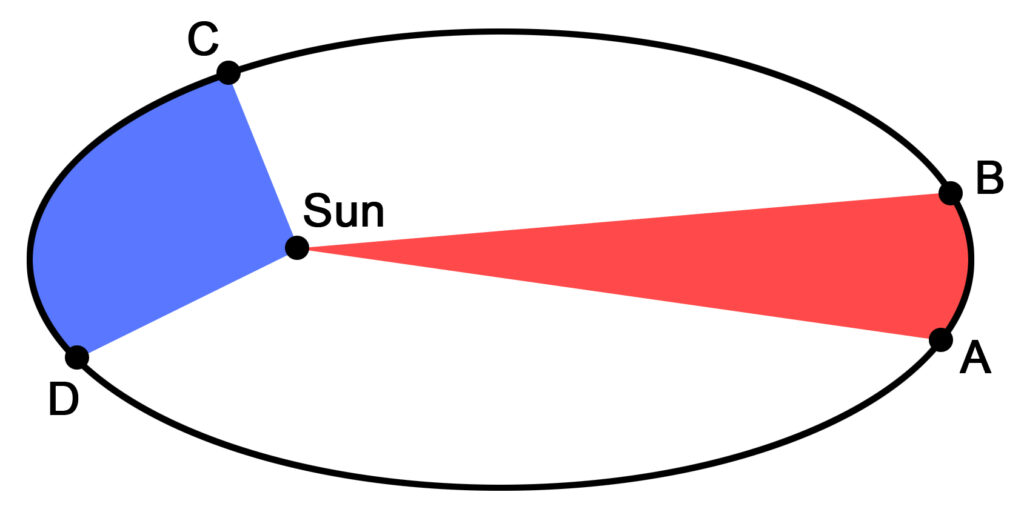
As was previously determined, the orbital periods of solar system-dependent objects vary to the 3/2s power of the proportional radius. Johannes Kepler’s third law of planetary motion states that the cube of a planet’s semi-major orbital radius is directly proportional to the square of the orbital period for that planet. The semi-major axis is the greatest distance traced out by the planets’ orbit. The semi-minor axis is the shortest distance to center for that orbit.
Kepler’s third law relates the orbit’s semi-major radius to the period of the orbit. One can form a sphere, or in the case of an elliptical orbit, an ellipsoid. The space volume of the object traced out by the orbit represents the spatial portion of Kepler’s equations while the surface area of the ellipsoid represents the period of the orbit.
If the orbit is circular, then the volume of the space portion of the circle is:
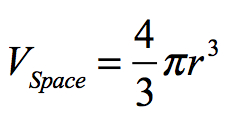
This formula represents the spatial part of the formula. The time aspect of the orbit under Kepler is represented as follows:
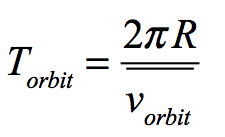
or the circumference of the orbit divided by the average velocity.
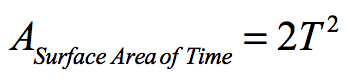
since the linear orbit (2πR) occurs in one orbital period T. The ratio of the spatial component of the orbit to the surface area of time is:
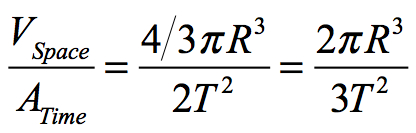
Since we are dealing with a ratio, constants for this formula can be eliminated leaving the formula for the approximate2 solution to Kepler’s 3rd law:
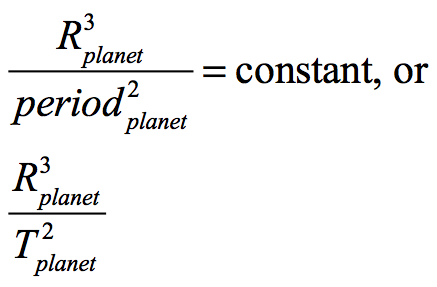
If we begin with Newton’s law for gravity, we can derive this relationship:
• From Isaac Newton we have the relationship between the force of gravity and circular motion (note that the velocity is the average velocity of the orbit):
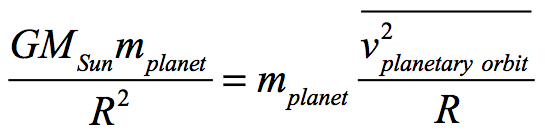
• The amount of time for one period:
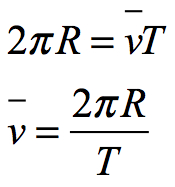
• Combine and simplify:
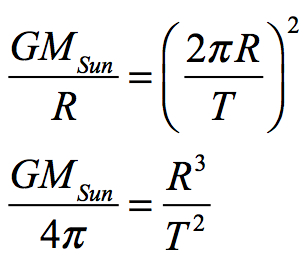
Since
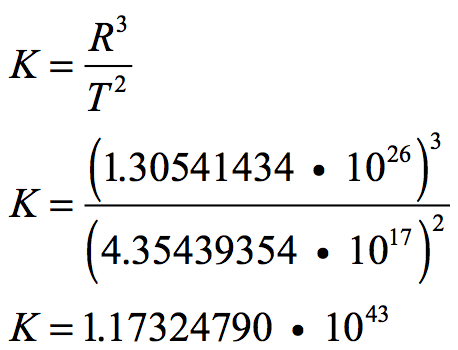
is a constant for our solar system, and no matter what planet is being measured,
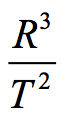
is unchanged for the solar system.3
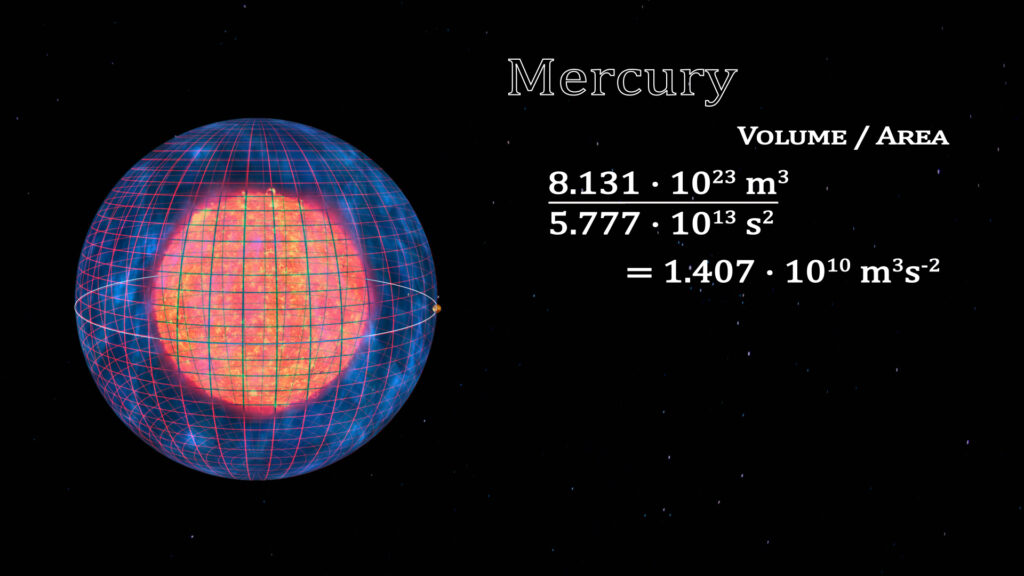
If we look at the solar system planet by planet, this constant can be deciphered. The volumes enclosed by a spherical (or elliptical) orbit is equal to the volume traced out by that planet’s orbit. We illustrate this by the cubing of the semi-major radius of the orbit of the eight planets. The surface area of time for these orbits is represented by the grid on the surface of the spheres. To the right is the ratios of the cube of the radius divided by the square of the orbital periods.
The constant for the solar system is 1.408 • 1010 m3s-2.


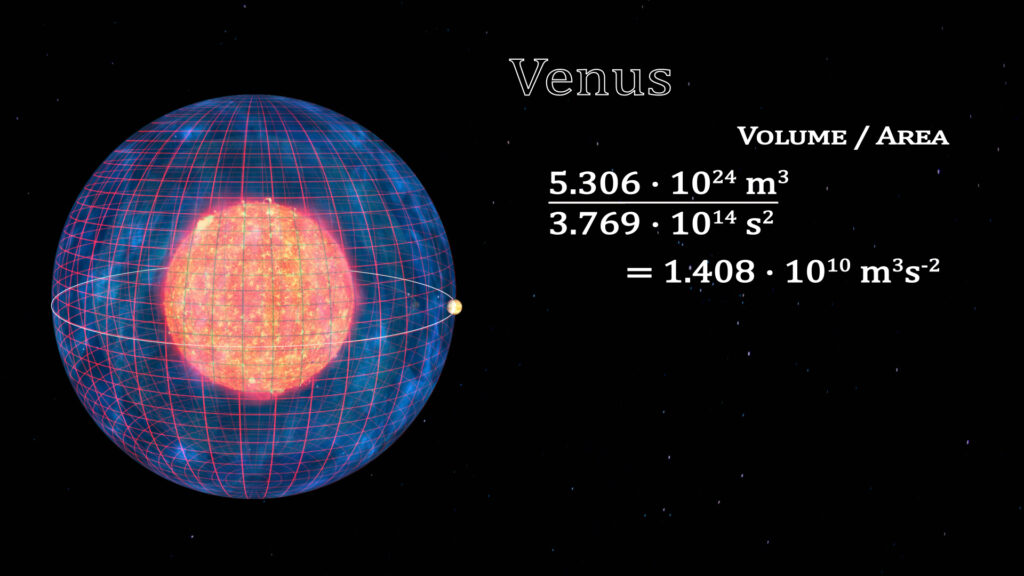
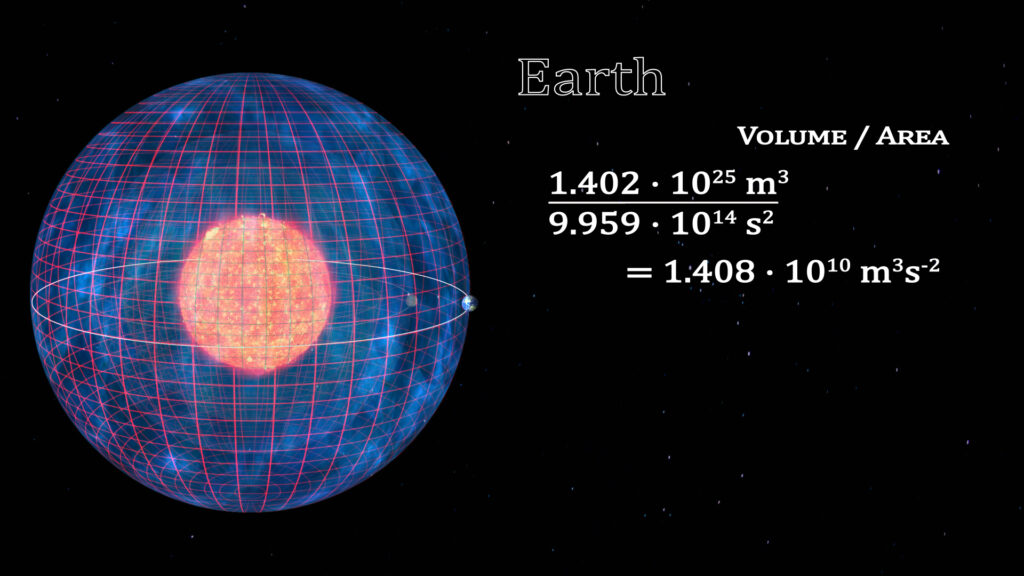
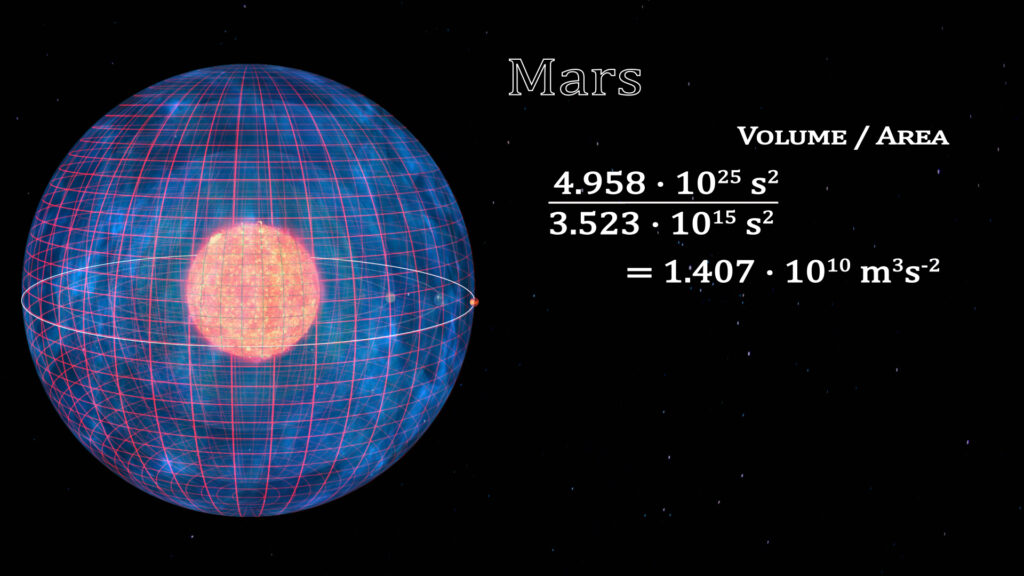
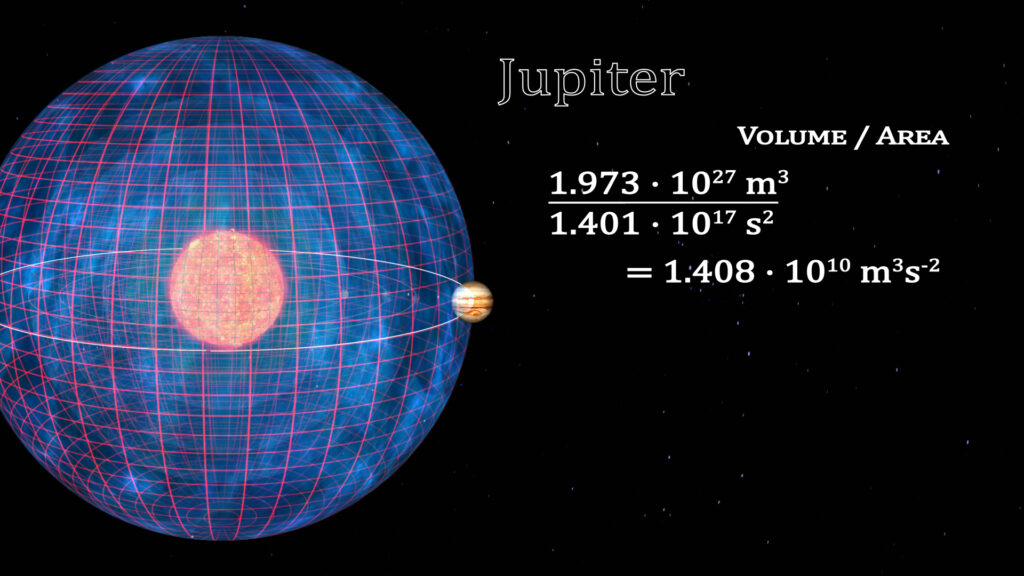
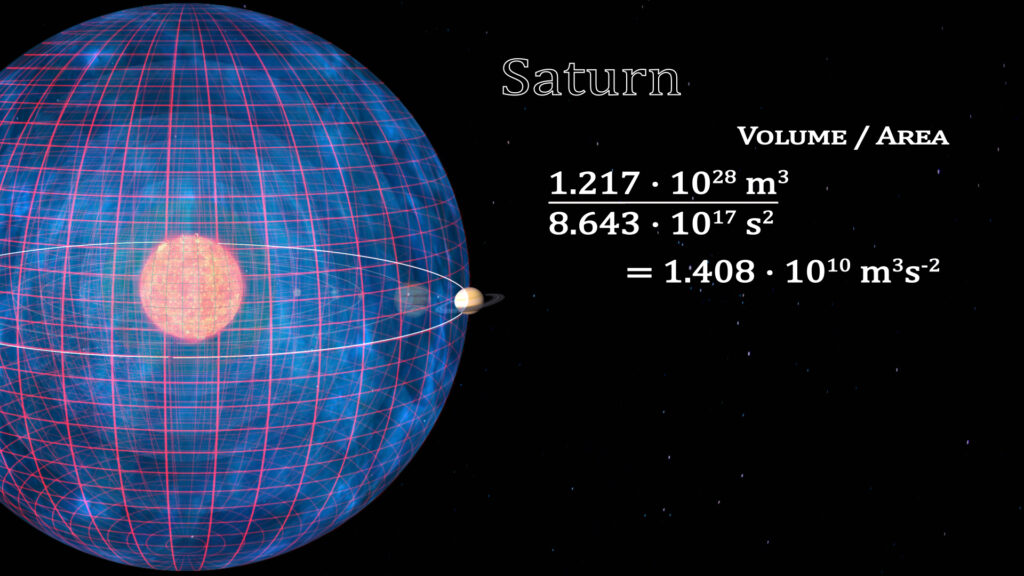
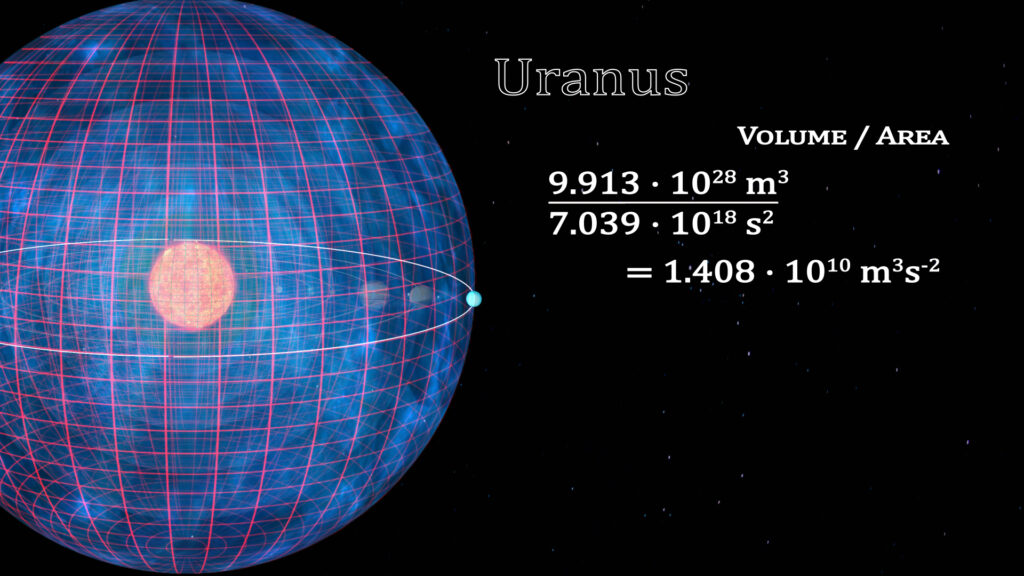

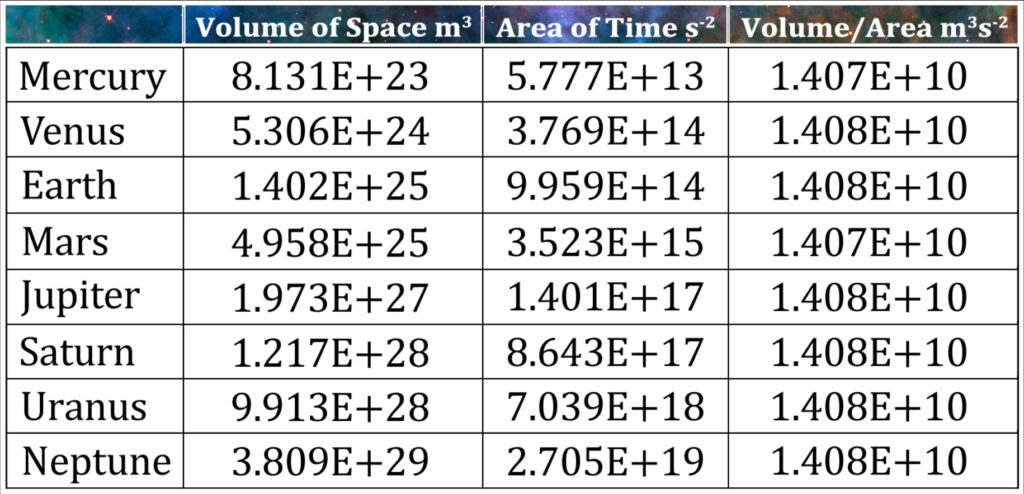
The Relationship of Space and Time Within a Gravitational System
Hermann Minkowski stated that a result of Einstein’s Special Relativity is that space and time are forever linked in what he referred to as spacetime. Ten years later Einstein carried this linkage to his formulations in General Relativity.
It is General Relativity that links spacetime to gravity, and it is this linkage that determines orbital periods. Time actually is the mechanism that determines spacetime’s force-like curvature. Time slows near massive objects. This curves spacetime and causes objects to attract.
The question becomes, what is the space and time connection for the Universe as a whole? Does the relationship between the Universe’s age and its size relate in the same way as that of any other gravitational system? The previous discussion of time indicates that it does. If time varies to the 3/2 power with the Universe’s radius, then the universal gravitational system should have a Keplerian constant that is identical to any other gravitational system.
The Kepler-Otto Universal Curvature Constant (K)
This proportional relationship holds for the Universe. The cube of the Universe’s radius divided by the square of the Universe’s age is a constant. This constant will be referred to here as the “Kepler-Otto Universal Curvature Constant”. Its symbol is K and its calculation is:
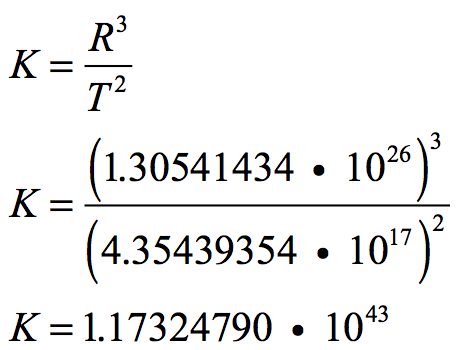


The Universal Black Hole
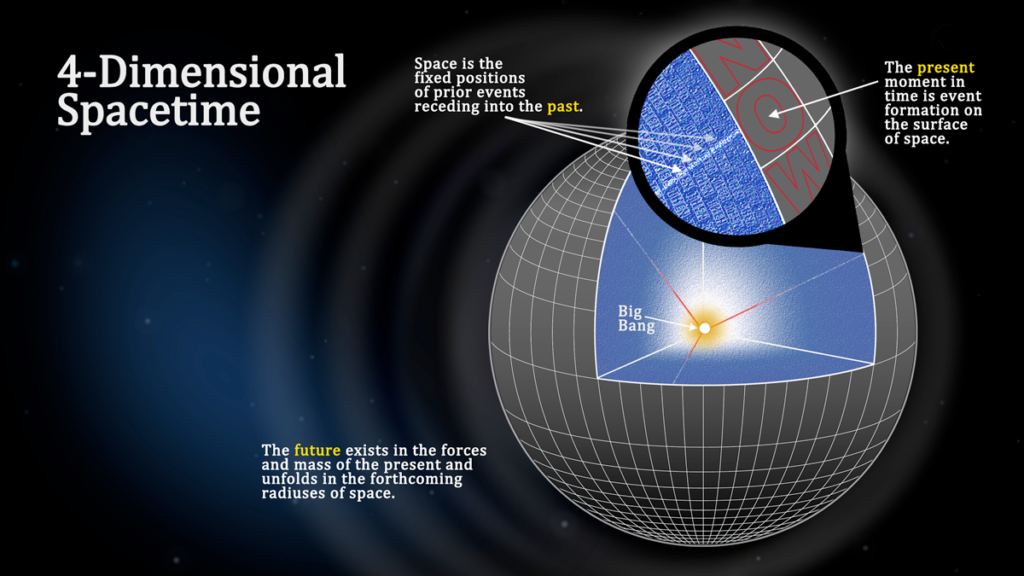
The spacetime relationship is due to a very specific aspect embedded into the nature of the Universal Black Hole. Time is the event horizon surface area of the black hole. Space is the volume within the horizon limit. It is the three dimensions of space contained within the Universal Black Hole and the surface area of the horizon that generates the events of time.
The event horizon is where the memory of all events of the Universe’s history are stored. It is also where all mass resides, i.e., mass only exists in the present, and the event horizon is the present radius of the Universe. The space inside of the event horizon is the past. No mass exists in the past.
Universe’s Curvature and Gravitation
It is the black hole nature of the Universe that generates the relationship between space and time. The physics of the Universe is a product of the expansion of the Universal Black Hole. K is a result of the relationship between the Universe’s spherical volume divided by its spherical surface area. Unlike Kepler’s law for planetary motion, when applied to the Universe as a whole, there is another relationship that comes from the Universe’s curvature; Newton’s gravitational factor (G).
G is a product of this curvature. When the Universe was smaller, the tighter curvature generated a higher G.
The units for G are:
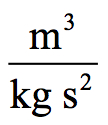
When G is multiplied times the mass of the Universe, it results in the same units as K. If the previously derived formula for the radius of the Universe is combined with the Schwarzschild formula for the radius of the Universal Black Hole, the result is:
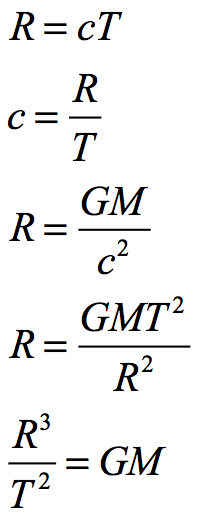
Therefore:
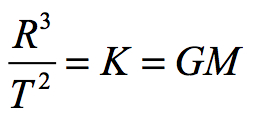
As the Universe expands, its mass increases. The higher mass necessitates an expanding event horizon. Therefore, G is inversely proportional to M such that GM equals K. Consequently GM is always constant.
Physics is Generated by the Universe’s Geometry
Once again we have the recurring theme: The laws of physics are generated by the geometry of the Universe. Mass, G, Radius & Time are all interlinked through one of the few true constants, which we refer to as K. The geometry is that of a black hole, and when that black hole is the Universal Black Hole, all of the rules of the Universe are its product. After all, the Universe is a closed system. It is the Universal Black Hole’s thermodynamic barrier at the event horizon that makes our universe a closed system, i.e., separate from all else.
Occam’s Razor Revisited
The entire presentation up to this point has been based upon the relationship of space and time. It is now shown that mass and the Newton gravitational curvature factor are all structured from this same relationship.

- G is not actually a constant. It is one of a number of factors that is dependent upon the current radius of the Universe.
- This is an approximate solution because the vast majority of the mass of the solar system is contained in the Sun, but the large gas planets, e.g., Jupiter and Saturn, contribute a minor amount of influence due to the mass that they contribute to the system. In addition, General Relativity alters the Keplerian relationship to a small degree.
- The mass of the planet is also a factor, but since the mass of the Sun is overwhelmingly larger than that of even Jupiter, the planet masses can be ignored for this rough calculation.
