Download this chapter for offline viewing (no videos, 1MB)
Download this chapter for offline viewing (includes video content, 6MB)
What if the velocity of light has not been constant over the history of the Universe? What if, as in other gravitational systems, c varies with distance from the gravitational center? Then, just as in planetary orbits, the velocity of light would vary to the -1/2 power with radius.
Orbital Speed
In regards to orbital speed1, Isaac Newton determined that the approximate mean orbital velocity is equal to the following formula, where m1 and m2 are the masses of the two body gravitational system:2
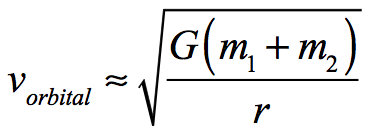
If one mass is significantly greater than the other as is the case with the Sun and the various planets, the approximate formula can be changed to:
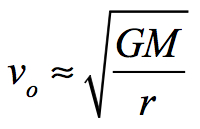
Where M is the mass of the larger mass, i.e., Sun.
Escape Velocity
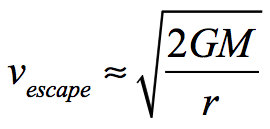
Note that escape velocity equals orbital speed times √2:
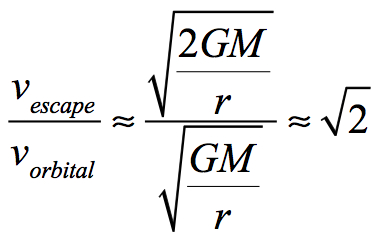
Keplerian Velocity
In spreadsheet 1 we calculated the radius of the Universe to be the current velocity of light times the age of the Universe. The base assumption was that the expansion rate of the Universe is the velocity of light. If this is true now, then in all likelihood it has always been true.
The velocity of light is the rate that spacetime is created. It is the rate that Minkowskian space is generated – the worldline between the events of time and the spacing of these events. Since gravity is a central force that pulls the matter of the Universe together, then in all likelihood the Universe’s expansion rate has decelerated. With the deceleration of the expansion the velocity of light must decline in an identical manner.
If R = cT, then c = R/T. This links the velocity of light directly to the radius of the Universe and its age. If time changes to the 3/2s power with radius, then the velocity of light must change to the -1/2 power with radius:
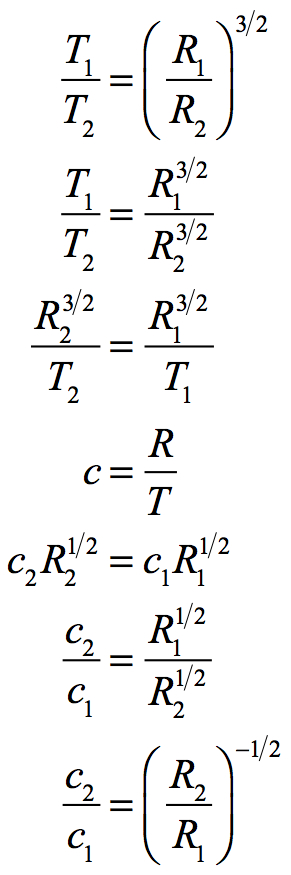
If we assume that the current relationship, where c = R/T has always been the case, then the velocity of light will always be the Radius of the Universe divided by the Age of the Universe, and c will change by the -1/2 power of the proportional change in radius. This is in keeping with Kepler’s third law of planetary motion.
Velocity of Light at the CBR Event
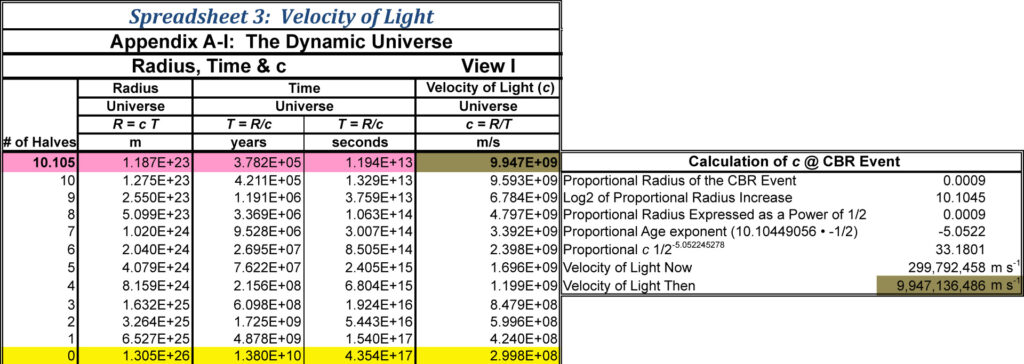
The radius of the Universe when it had cooled to the point that hydrogen protons could capture electrons was 1/1,100th the current radius. This is a little more that (1/2)10 its current radius (actually it was (1/2)10.44906 the present radius). If the velocity of light varies to the -1/2 power with radius, then its velocity was:

This approximates:
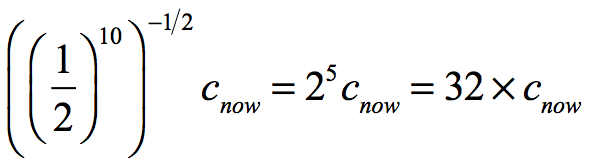
While intuitively this would seem to present a Universe from the past that would be unrecognizable to observers from the present, this is not the case. The velocity of light adjusts to a change in the rate of event creation, i.e., time flow, relative to the change in the radius of space. But everything is viewed from the perceiver’s own flow of time. All radiation from the past enters the present after adjustment to local time flow. Just as a shell observer near a massive object cannot directly observe another shell’s differential velocity of light, present-day observers cannot directly witness differential light velocities of the past.
Light’s velocity at the time of the CBR event was equal to the Universe’s radius proportion of that time relative to now to the -1/2 power, which is approximately 25 or 33 times that of today.
The Space-Traveler’s Paradox
A fixed velocity of light makes it so that there could be a velocity that could exceed the expansion rate of the Universe making it possible for a particle or light to circle the Universe and return to its source. We can refer to this as the space traveler’s paradox. If an astronaut travels in any direction for a very, very long time, they could theoretically circle back home if the Universe expanded at a rate less than c. The high velocity of travel would cause the traveler to age less than the Earth-bound inhabitants. Due to the circling around paradox, there would be two Earths.
One aspect that makes a universe a universe is the distinct set of thermo-dynamics unique to that cosmos. Cause and effect come into question for this type of universe. A Universe that expands at exactly the velocity of light and decelerates with the expansion eliminates any such paradox. No matter how fast a mass travels, the expansion always increases distances between objects making circumnavigation impossible, and thus keeping cause and effect in order.
The Henri Poincaré Model
Henri Poincaré was a preeminent mathematician, physicist and philosopher. He was a contemporary of Albert Einstein and contributed to applying the Lorentz transform to resolving difficulties with Maxwell’s wave equations. He proposed one of the most famous mathematical problems in history with his Poincaré conjecture. After a century of effort Grisha Perelman finally proved the conjecture in 2006.
He was also a great cosmological philosopher. In Excursions into Mathematics by Beck, Bleicher & Crowe3 the authors describe a universe seen by Henri Poincaré where a hyperbolic plane existed within a Euclidean plane as seen in the excerpt below:
“Euclidean geometry might, in fact, arise from conditions in the physical world. Poincaré imagines a universe consisting of the interior of a large sphere, say of radius R. He makes three basic assumptions:
1. In this sphere of radius ‘R’, the absolute temperature varies from a large value at the center to absolute zero at the surface according to the law that at any point at distance ‘r’ from the center the temperature is R2 – r2.
2. All dimensions of all objects in this universe are in direct proportion to the temperature.
3. Every object instantly takes on the temperature of the region in which it is placed.
This universe, which appears bounded to us, will appear unbounded to its inhabitants. For, as they walk toward the surface of the sphere, their legs – and hence their steps – become shorter and shorter, so they can never reach the surface.”
The universe described by Poincaré is virtually identical to the one described here. The “length of the legs” of the inhabitants in his universe is the same concept as put forward here. It is not only temperature that declines with the expansion. The velocity of light declines in a like way. The velocity of light changes due to an acceleration of the flow of time. The velocity of light’s decline makes objects increasingly inaccessible. In theory, there is no end to how low light’s velocity can become.
Poincaré also points out that “Every object takes on the temperature of the region in which it is placed.” The physics of all objects within the Universe instantly take of the characteristics of that moment. The Universe shares a common present defined by a single radius. In this way all physical functions are unified.
Poincaré also shows how a universe can be both infinite and finite depending upon whether it is viewed from within or from a higher dimensional plane. In this way a definable black hole can contain an infinite universe within.
- Technically, orbital movement is referred to as speed since velocity is a vector function. Orbits have a constantly changing space vector. From another perspective, orbiting objects do follow a straight line within the curvature of spacetime.
- General Relativity varies slightly from Newtonian mechanics.
- Anatole Beck, Michael N. Bleicher & Donald W. Crowe, Excursions into Mathematics, A. K. Peters, Ltd., Natick, MA 2000, pp. 303, 304
