Download this chapter for offline viewing (no videos, 4MB)
Download this chapter for offline viewing (includes video content, 111MB)
Planck-Wheeler’s energy and mass unify quantum mechanics and General Relativity. Planck-Wheeler mass and energy are both smaller than the total mass and energy content for the Universe, but these values are not minimum values for either mass or energy. The extrema quantities are based on the minimum energy of an electromagnetic wavelength – one with a wave radius equal to the radius of the Universe. This minimum quanta is named here Planck-Otto energy and mass. Herein lies the information content of the Universe.
Redshift of Light Exiting the Event Horizon of a Black Hole
When a mass freefalls towards the event horizon of a black hole, as seen from an observer in flat spacetime, the viewed freefall appears to accelerate at first, but as it makes its final approach, it slows down. Finally in the last phases of freefall, it appears to freeze at the hole’s horizon. The light from the fallen object redshifts as it climbs out of the deep gravity well. Finally, the light redshifts beyond observation at any frequency. This is due to the slowing of time towards zero relative to the time flow of the distant observer in flat spacetime.
The question becomes, “How far does the light redshift?” In theory, the light’s wavelength would shift to infinity. But is this the case? The attenuated wavelength has a limit, and that limit is the radius of the Universe. The final light from the lost mass at the horizon of the black hole spacetime stretches until the half wavelength reaches this limiting radius.
Planck-Otto Energy and Mass
What is the minimum possible energy for an electromagnetic waveform? It is an impulse with a wave radius equal to the radius of the Universe. No lower energy can be obtained. Beyond this extrema no wave can form. Planck-Otto’s energy is calculated:
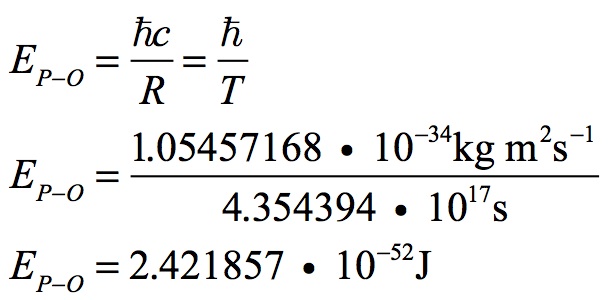
Planck-Otto’s mass is the conversion of this energy to the mass equivalent:
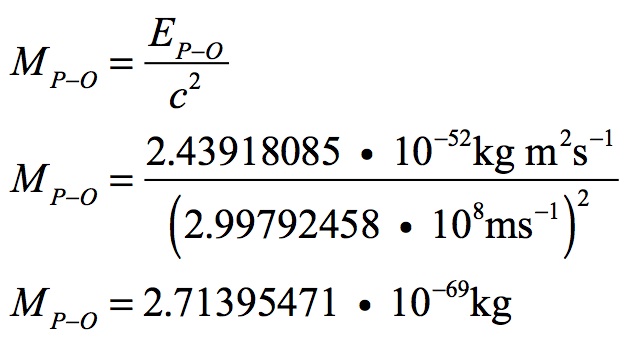

Changes over the History of the Universe
It has been established that the age of the Universe has changed to the 3/2 power with radius. The radius of the Universe and its relationship to time has also been determined. What hasn’t been established is the variation of Planck’s angular momentum since the Big Bang. As will be later seen, Planck’s angular momentum has changed to the -1/2 power with radius. With this information Planck-Otto’s energy can be determined by the proportionality of these factors to the Universe’s radius:
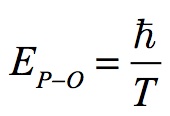
The symbol for proportionality is ∝.
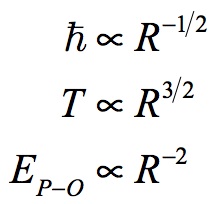
Likewise Planck-Otto’s mass can be calculated using its proportional relationship to other factors:
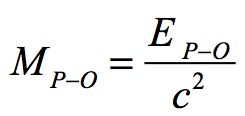
Planck-Otto’s mass has changed as follows:
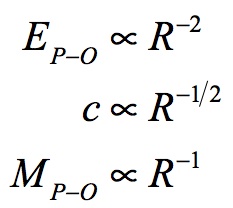
Planck-Otto’s Energy and Mass at the Time of the CBR Event
Since the Planck-Otto quantities result from the energy of a wavelength the radius of the Universe, that radius can be used to calculate these quantities. The radius of the Universe has been calculated for the time of the cosmic background radiation release. When combined with the proportional changes in the age of the Universe and Planck’s angular momentum, Planck-Otto’s energy and mass can be calculated for this time:
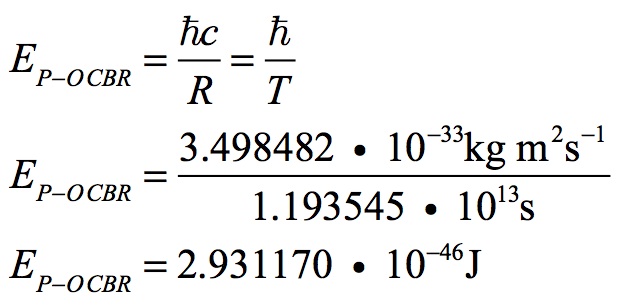
Planck-Otto’s energy has decreased with the square of the radius of the Universal Black Hole. Although this quantity is rapidly becoming less, its importance never diminishes. It is the source of the Universe’s information.
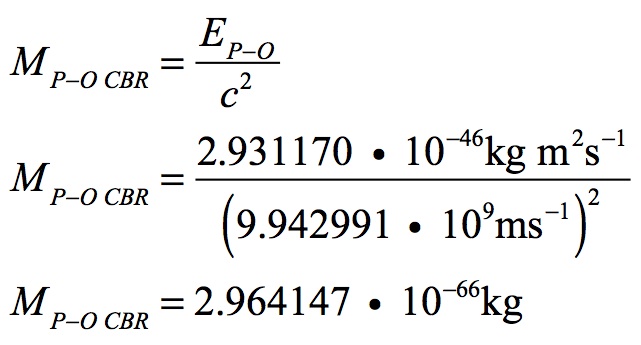
While Planck-Otto energy varies to the inverse square of radius, Planck-Otto mass varies inversely with radius.
Planck-Otto’s Energy and Mass at the Time of the Big Bang
Applying the same technique the Planck-Otto quantities can be identified for the Big Bang.
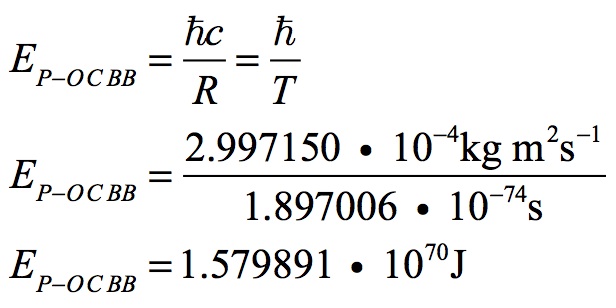
Note this is the same energy content as existed for the whole Universe. Planck-Otto’s energy marks the energy of the first event, but at the Big Bang the Universe was only one event old. Therefore, the two quantities are the same.
Planck-Otto’s mass can be calculated in the same way as before:
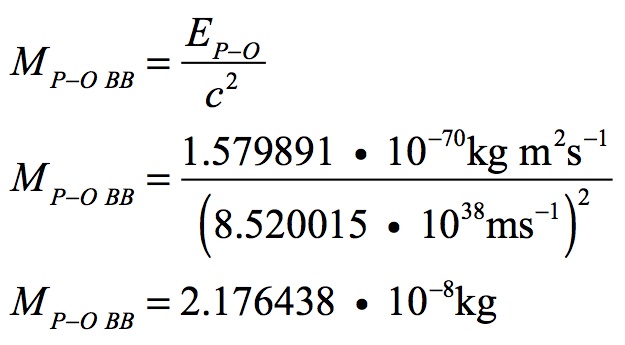
Note that Planck-Otto’s energy was 121 orders of magnitude greater at the Big Bang than it is today while Planck-Otto’s mass was 60 orders of magnitude greater.
Light’s Quanta
The Planck-Otto extrema are more than curious concepts with no meaning in physics. They are the foundations of the quantum nature of the Universe. This becomes evident when looking at light. When light travels through the Universe, it loses energy. This is due to the expansion of space while light is in transit.
Until now, there has been little explanation of the mechanism for this loss. One of the most sacrosanct principles of physics is that energy is conserved at all costs.
A prime example of this effect is the change in the energy level of the “black-body radiation” since the CBR event. When the temperature of the Universe cooled to 3,000 K 378,000 years after the Big Bang, hydrogen captured the free electrons and became neutral. At this point the space became locally transparent.
We see this event today, but instead of the apparent black-body temperature of 3,000 K, the observed black-body temperature is 2.725 K. This wavelength increase results in a reduction of light’s energy. Light with an initial wavelength of 7.9 • 10-7m now has a wavelength of 8.7 • 10-4m.
In the dynamic Universe Planck’s angular momentum has changed as has the velocity of light. This is due to the change in the movement of time relative to the radius of the Universe. Since time changes to the 3/2 power with the change in the Universe’s radius, time-dependent factors, e.g., Planck’s angular momentum and the velocity of light, also change.
The energy of the light has dropped by a factor of 1/1.211 • 106 since the CBR event. It is interesting to note that the energy decline is much greater than what would be expected by the 1/1,100th ratio of the wavelengths. This is due to the change in Planck’s angular momentum and c. The electromagnetic attraction between the hydrogen nuclei and the free electrons was also determined by the physics of that epoch of the Universe. This is not apparent to us from our present vantage point. All factors changed in the exact proportion to make the ancient Universe appear to have the same factor values as it has today. Since we view the past through the flow of time today these different values are not apparent.
The main question here is, “Where does the lost energy go?” Light dissipates its energy as each wave completion releases a Planck-Otto energy wave. If light had a frequency of 1.2602 • 1016 s-1, then 2 × 1.2602 • 1016 Planck-Otto waveforms1 were generated per second. At the time of the CBR the primordial Planck-Otto energy was 2.956334 • 10-46 J for each waveform. Cumulatively, these released waveforms reduced the energy to the present day observed values. Energy is lost as Planck-Otto quanta take energy from the electromagnetic wave pulse, leaving the lost energy in the mass of space.
Light doesn’t get “tired” as one theory for this effect proclaims. It loses discrete quanta for each 1/2 waveform. This quanta is the Planck-Otto waveform.
| Comparison of the Light from CBR Event Then & Now | ||
|---|---|---|
| current CBR wavelength | λnow | 8.6824 • 10-4 M |
| initial CBR wavelength | λCBR = 1,100 × λnow | 7.8931 • 10-7 M |
| wavelength ratio | λnow/λCBR | 1.1000 • 103 |
| current CBR frequency | ωnow = λnow/cnow | 3.4529 • 1011 s-1 |
| initial CBR frequency | ωCBR = λCBR/cCBR | 1.2602 • 1016 s-1 |
| frequency ratio | ωnow/ωCBR | 3.6498 • 104 |
| current CBR energy | Enow = ħnow × ωnow | 3.6413 • 10-23 J |
| initial CBR energy | ECBR = ħCBR × ωCBR | 4.4097 • 10-17 J |
| energy ratio | Enow = ECBR/Enow | 1.2110 • 106 |
The Universal Black Hole Zero Layer
The new paradigm for the functioning of a black hole, which is so much a part of this theory, provides a unique structure. When matter approaches the event horizon of a black hole, it is completely disrupted by the tidal forces. In the final stages of the approach, all of its energy is radiated in a process called de Broglie radiation. Ultimately, this radiated light’s velocity slows to zero relative to a distant observer.
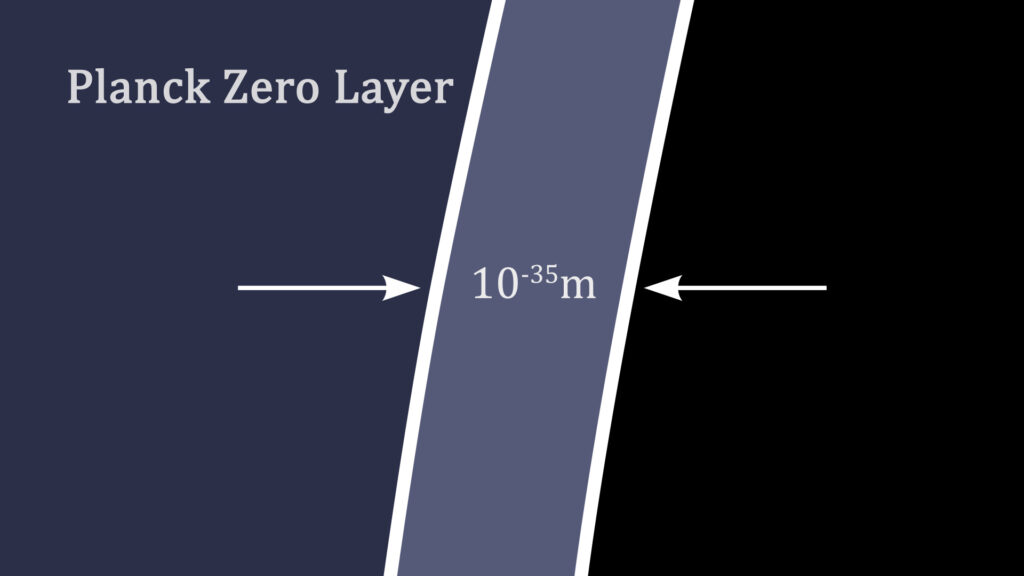
When light’s wavelength reaches Planck’s radius above the event horizon, it can no longer complete a waveform. Light’s relative velocity decreases to zero, even as its local velocity remains that of light, time movement ceases and acceleration becomes infinite. The light’s quanta become trapped in a quantum margin. This margin is called the zero layer. This is the place where no new waveforms can be formed. What remains is the quantum potential.


The zero layer separates the physics of the universe where the black hole formed from the universe within. The zero layer separates the two thermodynamic systems. The cause and effect of the outside universe have no direct effect on the universe within.
This is the case for our Universal Black Hole. Its experiences are separated from its progenitor black hole. The zero layer makes the Universal Black Hole possible.
The zero layer is uncompleted quantum potential. It is the black hole’s event horizon. It is a standing wave that surrounds the black hole. A standing wave is a form where the wave potential reflects back on itself. Self-interference generates quasi-stable waveforms.
This happens in the zero layer. The summation of the individual quanta that make up the horizon oscillate around the entire black hole.





e and i
e is a uniquely useful number. It has numerous applications in mathematics and physics. e like π is a naturally occurring transcendental number. If ax is plotted for different values of a on an (x, f(x)) coordinate plane, and if the derivative of a is also plotted, there are different results. For numbers above a certain level, the derivative plotting is above the non-derivative graph. For other number values of a below a certain level, the derivative plotting is below the non-derivative. The question becomes: At what value for a does the derivative yield the same plotting as its non-derivative?
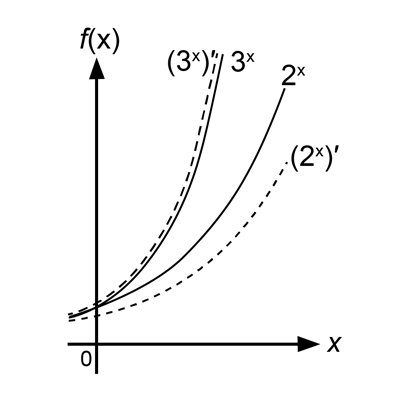
When calculated, as it is with π, there can only be an approximation to progressive degrees of accuracy. The number that produces the same graph is 2.718281828…. This has been designated as e.2
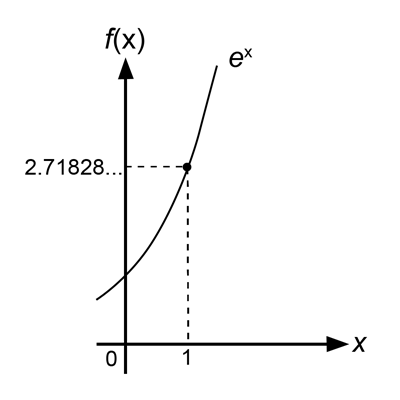
e is the preferred base for logarithms. For purposes here, it is the number whose differentiation and integration yield the same result:

This is a powerful tool. It means that if there is a series of differentiations or integrations, as with a wave equation, ex remains intact. This simplifies mathematical expressions immensely.
i is the symbol for an imaginary number. It is equal to √-1. Since this is not calculable in real numbers, it is considered imaginary. But i can be a powerful tool. It enables us to build in oscillations into equations.
Oscillating functions usually employ trigonometric functions with sines and cosines. Here is where i comes in. i mirrors the oscillation of sines and cosines because when it’s squared it becomes -1 and when taken to the 4th power it returns to 1.
Leonhard Euler developed his formula around e and i. It is Euler’s formula:
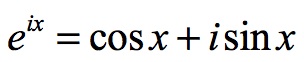
Plotting on the Gaussian Plane
The plotting of this function requires a coordinate system that includes i. For this the Gaussian plane, also known as the complex plane, is used. Here the x-axis remains entirely of real numbers. However, the y-axis now becomes a plotting of the complex numbers iy.
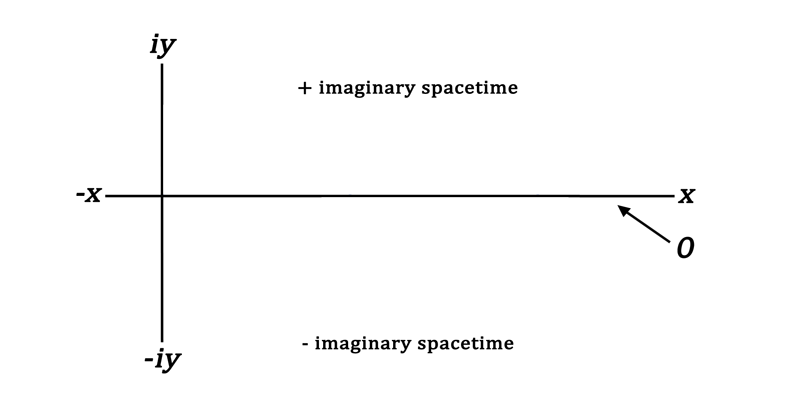
Beginning at the axis point for x = 0, ei0 = 1. When the first four derivatives (indicated by ’, ’’, ’’’, and (4)) of this equation are taken, the following is seen:
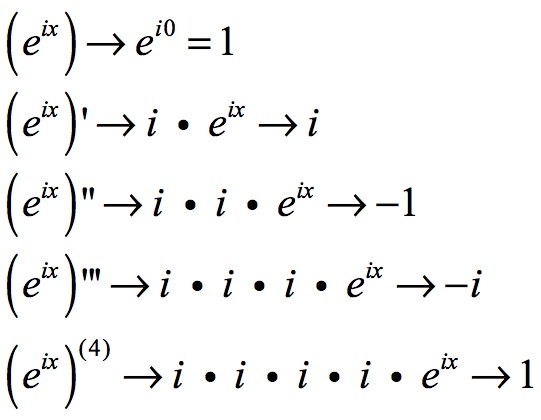
The plotting of the above waveform is:
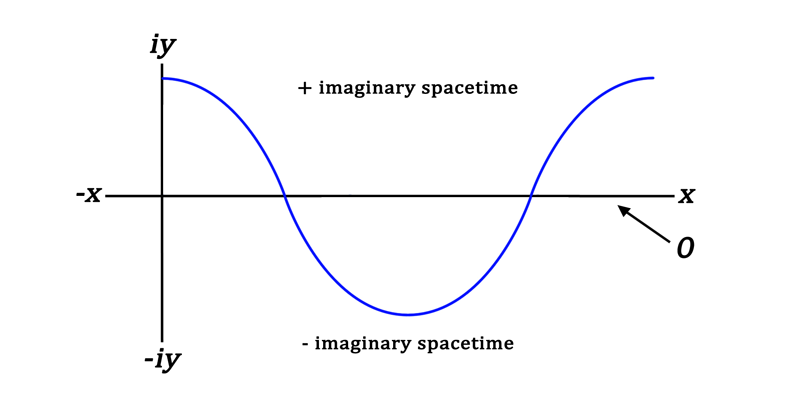
The Zero Layer and Event Creation
The plotting of the waveform using e and i seems just a matter of the employment of a mathematical trick to represent the oscillating wave. Imaginary space would seem to have no relationship to the real physics. Physics is based on real numbers.
When we look at the foregoing graph, ask if there are any real numbers represented here. At first it may not be apparent, but look closely. In reality, there are two points of every waveform that result in real numbers. These are when iy is equal to 0. There are two points for every waveform anchored in the physical reality of the Universe’s spacetime.
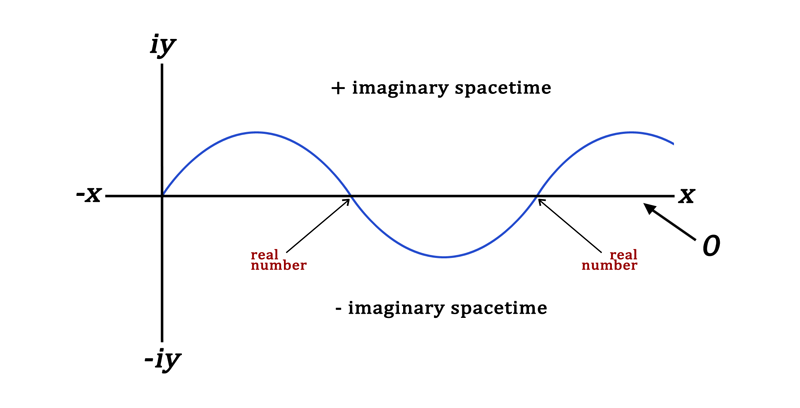
Every instant when the waveform crosses the x-axis, an event is created.
All events are generated on the event horizon as the name would indicate. The event horizon is surrounded by the zero layer. The zero layer is imaginary space relative to the “real” Universe. When it crosses from imaginary space to real space twice in the waveform, an event is created each time.
Discrete events are created when there is an exchange of mass and energy via E = mc2. For each such exchange a Planck-Otto energy wave is released. This quantum release of energy is the reason that light loses energy while in transit across the Universe. Light doesn’t stretch away its energy. It loses discrete quanta with every waveform.
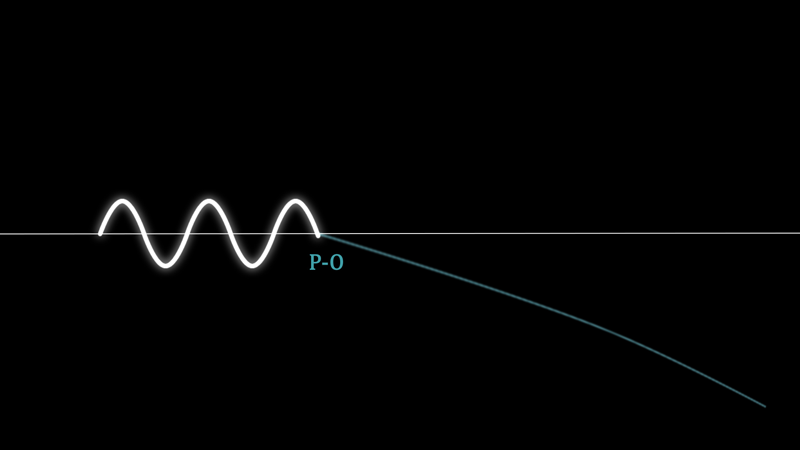
A phenomena related to synchrotron radiation caused by the negative acceleration of the expansion (A) causes the release of the Planck-Otto waveform. There is a mass ⇄ energy exchange for each waveform node.
The progenitor black hole fills the zero layer with potential. The universe within extracts that potential from its own perspective on the zero layer. The gift from the parent black hole is its mass sorted through the quantum mechanics of the product universe.
Quantum mechanics and General Relativity merge on the surface of the Universal Black Hole. Phenomena like quantum tunneling, action at a distance, and radio waves traveling through solid objects can all be accounted for with the wave portion spent in the imaginary quantum probability space of the zero layer.
Just a Memory
Every waveform in this Universe leaves behind two events marked by the emission of a Planck-Otto waveform. The emission of this waveform leaves a discrete address within the Minkowskian spacetime grid marking both the three spatial coordinates and the radial time component of when the P-O waveform was released.
Every Planck-Otto waveform has two nodes. The first node is anchored in the Minkowskian grid of spacetime and the second is sent from that point to the radius of the Universe. The uncertainty of a waveform with a radius equal to R places the aspiring node on the present surface of the expanding Universe, but with an indefinite location. In this way the wave’s mass-exchange event is recorded. The information is left forever on the expanding surface of the Universe. The event becomes part of the Universe’s history of experience.
Werner Heisenberg established with his famous “uncertainty principle” that the more you know about one of two inter-dependent aspects of a quantum characteristic, the less that you know about the other. For example, by fine-tuning the calculation of the momentum of a particle (p), one loses knowledge about its location (x). His famous formula:
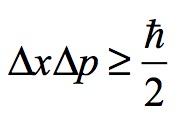
The magic of the Planck-Otto waveform is that it represents the ultimate exploitation of this law. The Planck-Otto waveform is a half waveform with two nodes anchored in reality. The one node is the location in Minkowskian spacetime. This location is absolute and unchanging for it is a point in the past where things cannot be changed and can be identified under the Principle as:
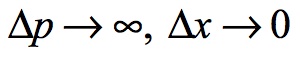
The other end of the waveform is stretched to the radius of the Universe. The momentum of this waveform is determined by the radius of the Universe at that moment. Momentum is therefore absolute, while location is completely unknown.
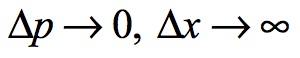
Therefore, the absolute location of an event in this Universe is recorded forever and that information is preserved by the Universe and can be read through a mechanism that is unknown everywhere within the confines of the Universe.