Download this chapter for offline viewing (no videos, 7MB)
Download this chapter for offline viewing (includes video content, 61MB)
One most sacrosanct principle in physics is the law of the conservation of energy. The Universe is a closed system. While mass has increased during the Universe’s expansion, energy has remained constant. Under General Relativity, energy in a gravitational system is a constant of motion. Energy may change from mass to momentum depending upon vantage point, but the combined potential and kinetic energies is always preserved.
Energy
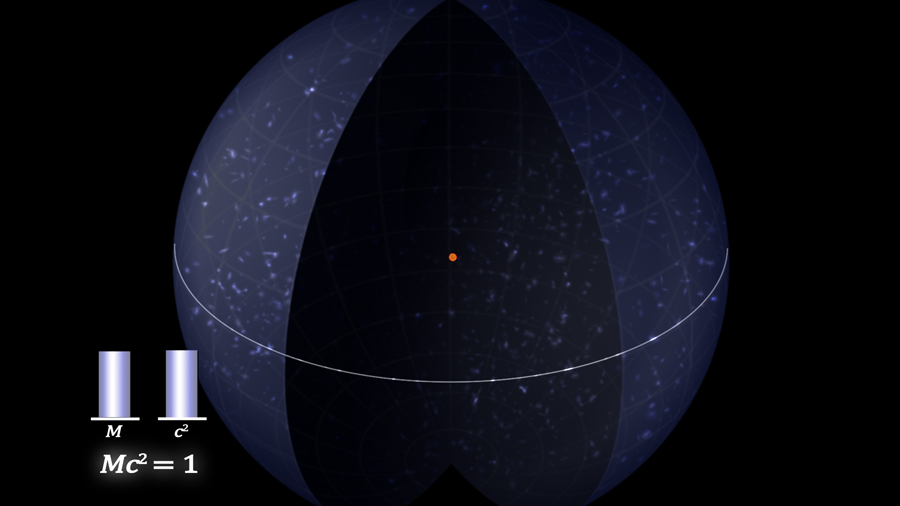
Energy can be summarized by the most famous formula in physics: E = mc2. For massless particles, i.e., photons, energy is equal to the frequency times Planck’s constant: Elight = ωħ. Mass in motion has momentum relative to a mass with a different vector of motion. The formulation for this is: E = γm0c2. Here m0 is mass at rest. Gamma is equal to:
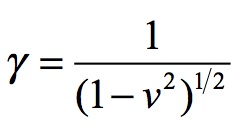
This is the Lorentz transform adjustment to energy for that mass’ relative velocity.
All energy has a mass equivalent. Movement is relative to a vantage point, but when moving with the mass there is only the rest mass. Even electromagnetic energy depends upon whether the source of the light is in motion towards or away from the observer.
One aspect of the black hole model for the Universe is that the vantage point doesn’t matter. Matter or electromagnetic waves all are part of the mass of the black hole. Even massless photons contribute to the hole’s mass. If we observe a black hole within this Universe, everything that is captured within the event horizon of the hole is part of its mass. This includes the light that cannot escape its hold.
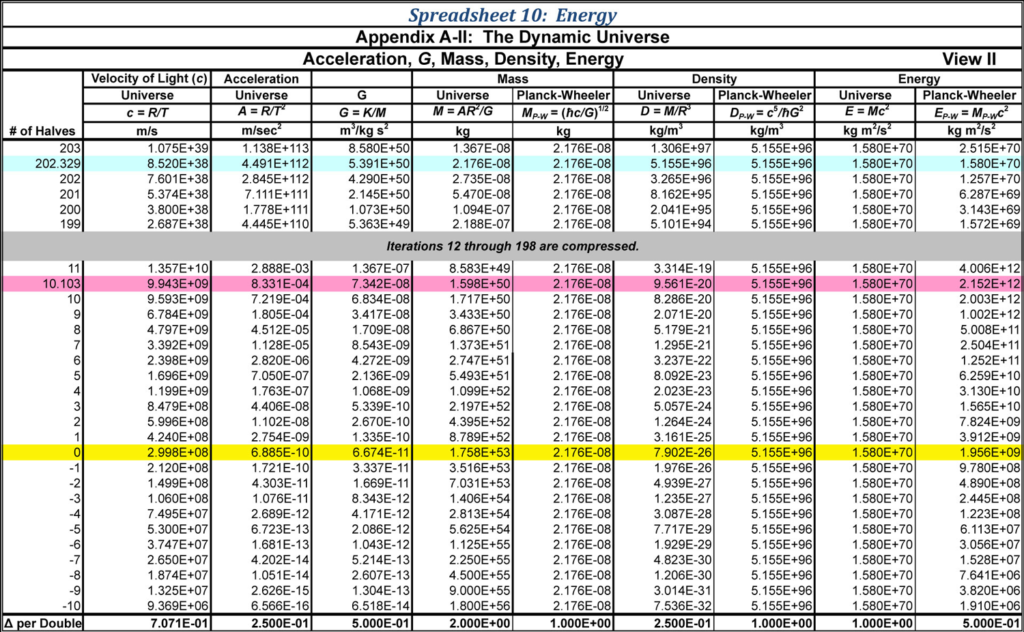
The Universal Black Hole’s mass is inclusive of its free energy and its conserved energy in matter or “dark matter”. For this reason the energy formula for the Universe is E = mc2. Since we know the mass of the Universal Black Hole to be 1.7578654 • 1053, then the total energy of the Universe is:

Law of Conservation of Energy
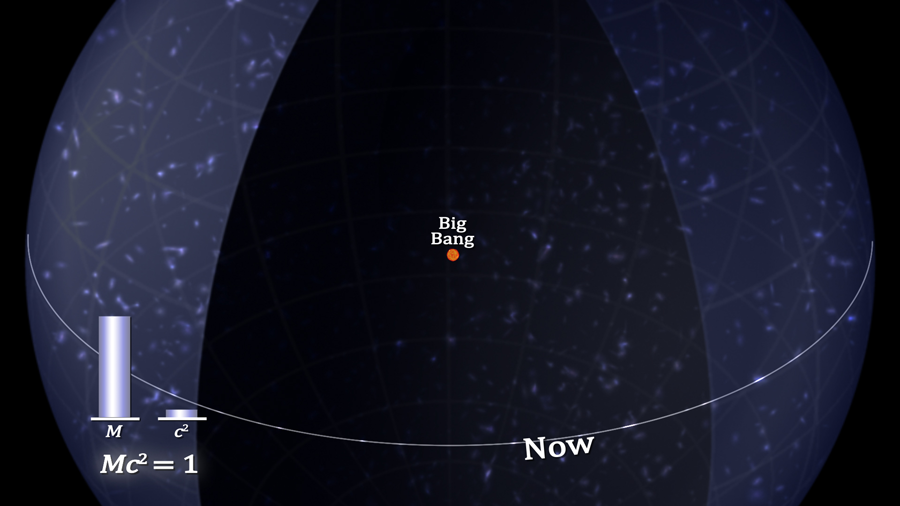
How has energy varied over the history of the Universe? Mass has increased linearly with the expansion, but has energy likewise increased? If we use the mass at the Big Bang and the velocity of light at that time and calculate E, it becomes apparent that energy has remained unchanged for the entire life of the Universe:
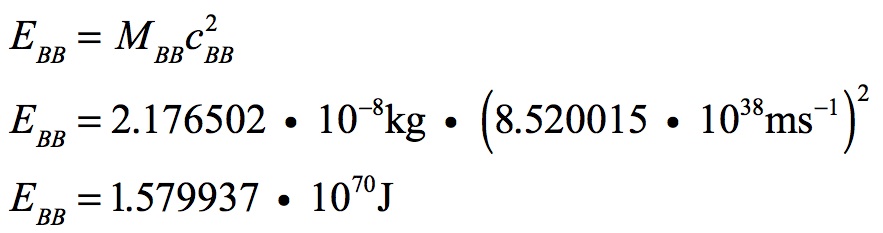
Even though mass has grown by 60 orders of magnitude over the Universe’s life, the total energy for the Universe has remained unchanged. This is due to the vastly higher velocity of light for the early Universe. Energy is conserved for the Universe as it is for any isolated system.
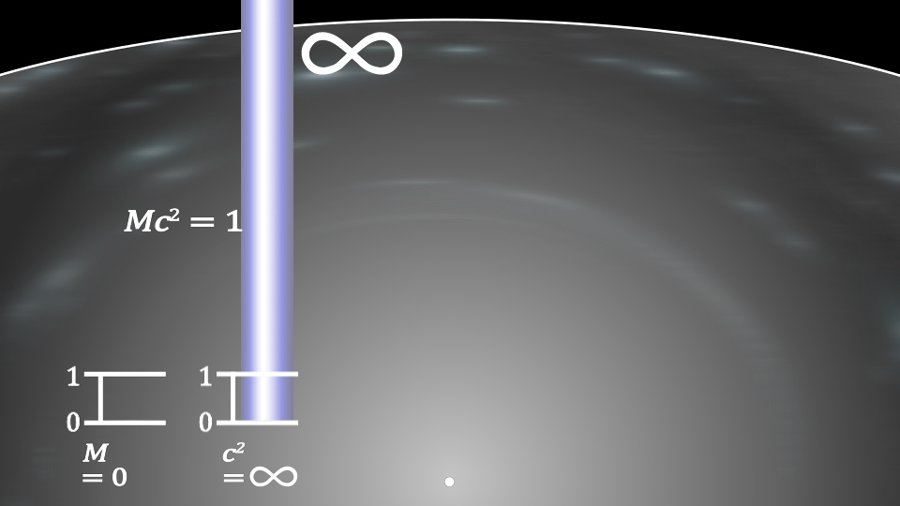
If we stand back and look at the model, it makes sense. The Universe at the Big Bang had a Planck-Wheeler mass of a 10-8 kilograms; not 1053 kilograms. This mass was compressed into a space with a radius of 10-35 meters. This is Planck-Wheeler’s density, 5.154886 • 1096 kg m-3.


It makes a lot more sense to compress the mass less than a grain of sand to this black hole density than to compress all of the stuff of the Universe into a Planck radius. To put this into perspective a look into the static mass and constant velocity of light model yields some insight. Imagine taking the mass of the Universe with its billions of galaxies each with billions of stars and compressing it into a radius 20 orders of magnitude smaller and a volume 60 orders of magnitude smaller than an electron. This makes absolutely no sense.
This is a critical principle. Mass is not fixed while energy is. There seems to be considerable speculation but little consensus of what was the mass of the early Universe. Most would agree that initial densities would meet Schwarzschild’s density parameters for a black hole, yet various explanations have been advanced to say why a black hole was not formed.1
This model resolves that problem. Mass has increased as time has accelerated. The slow time flow of the past resulted from a much higher velocity of light. It is the proportional shifting of the relationship between these two components of energy that resolves the conflicts with the intuitive aspects of theory.
It is the extraordinarily high velocity of light at the Big Bang that enabled the energy of the Universe to remain the same. Energy is conserved at all costs.


Energy is a Constant of Motion
A basic tenant of gravitational systems is that energy is a “constant of motion”. When a mass falls from a great distance towards a massive object, it accelerates and gains kinetic energy, but it loses potential energy. If two large masses are close to each other but separate, their combined gravitation will be the same as when combined.
When viewing a mass from a distant vantage point, falling towards a black hole, it will accelerate at first, but when it falls to close proximity of the hole’s horizon, it appears to slow. Ultimately, it will appear to freeze on the horizon, where its light will quickly redshift beyond view.
However, if the same falling object is viewed by a proximate shell that the mass is passing, the velocity of that object will appear to continue to accelerate. Movement at the horizon is at a mandatory velocity of light. But the same object when viewed from afar, appears to approach a zero velocity at the horizon. Even from this vantage point the energy of freefall is not lost, it shows up in the potential energy of the gravitation of the black hole.

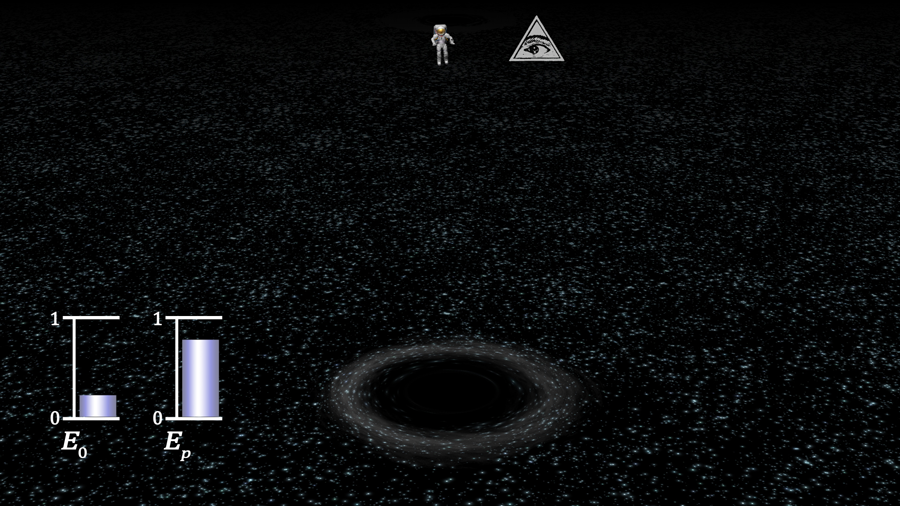

Energy for the Universal Black Hole is a Constant of the Expansion
According to the current paradigm for black holes, freefall within the horizon maintains the energy of the falling mass. Energy remains a constant of motion in all ways for a gravitational system.
For the Universal Black Hole expanding under Occam’s Razor’s principles, energy maintains this “constance of motion” principle. The energy changes from low mass at a very high velocity at the Big Bang to the present mass, which is sixty orders of magnitude greater with a velocity of expansion, i.e., c, that when squared is sixty orders of magnitude less. Kinetic energy converts to mass.



Planck-Wheeler Energy
Planck-Wheeler’s mass is the unique mass that produces both a Planck-Wheeler’s radius event horizon and produces a Compton’s wavelength equal to that same radial distance. The energy equivalent today for this mass is:
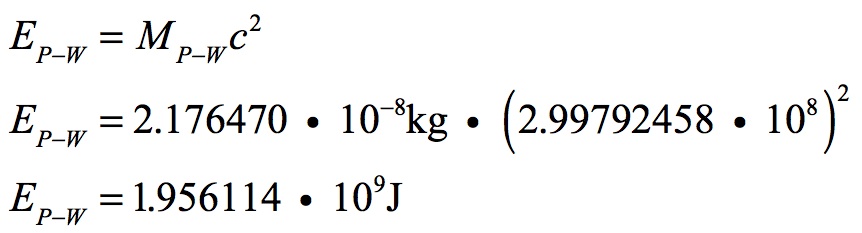
Planck-Wheeler’s mass was the same at the Big Bang as it is today except that the velocity of light was 30 orders of magnitude greater than today. Therefore, Planck-Wheeler’s energy at the Big Bang was:
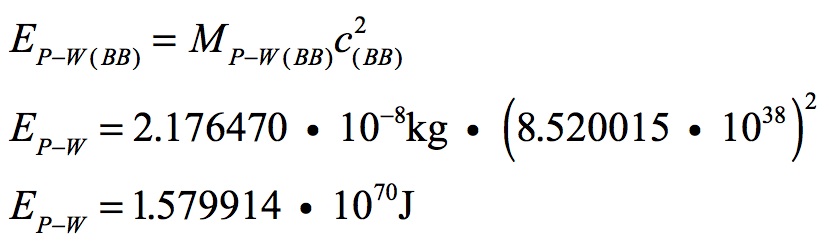
This is the energy content of the entire Universe:
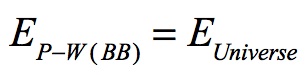
Planck-Wheeler’s energy and the energy of the entire Universe were the same at the Big Bang, these values have since diverged by 60 orders of magnitude since that event.