Download this chapter for offline viewing (no videos, 3MB)
Download this chapter for offline viewing (includes video content, 47MB)
What if events are separated from each other by space and time, thus forming a classic Minkowskian spacetime grid? What if all the Universe shares a common present? What if these events of the common present share an identical Minkowskian distance from the Big Bang? If we assume that the Big Bang is just another event, nevertheless the first event, this event point will have a specific distance (interval) from the present. We will call this interval R. Since the Minkowskian interval for a mass with its own past is the passage of time multiplied by the velocity of light, what if R is simply the fastest velocity in the Universe multiplied by the time that the Universe has expanded?
What is Radius?
Radius is a very familiar concept. Since most astronomical objects are either spherical or elliptical, the radius of those objects is clearly defined and dependent upon which radial angle is being measured. Based upon these examples, the concept of radius is quite easy to understand. It is simply the distance from the geographical center to the surface of the object.
But the determination of the radius of the Universe is more problematic. The Universe has no clearly defined edges. Wherever an observer is, the Universe radiates from that point. Several hundred years ago, it was popularly believed that if one sailed too far, they would fall off the edge of the Earth. Later that concept fell apart as it was learned that the Earth curves around on itself.
With the Universe that same dilemma exists. The solution is not so different than that discovered by the early explorers. Wherever an observer is, there exists a radius to the limit of the Universe. It would seem that we have not one radius but an infinite number based on where the measurement occurs. We are left with the same uncertainty. Where are we measuring from and to where are we measuring?
Another dilemma is the distinction of what radius is being measured. Is it the radius of the observable Universe or the entirety of its dimensions. Observability is limited not only by the measurement technology of the observer, but it is also constrained by the time that it takes light to travel from distant reaches of the Universe. Light can travel only so far since the formation of the Universe. Light’s velocity is limited so there are regions of space that are unobservable.
We can observe distant galaxies with light that left millions or billions of years ago, but we see stars that may no longer even exist. So we see the past and not its current appearance. Even seeing the observable Universe has problems related to what is seen.
If unobservable regions are included, an entirely different radius is at stake. This radius depends upon the operative theory of physics used. Inflation theory generates a much greater radial limit than the observable universe. Other theory variations derive results that differ from each other by many orders of magnitude.
Since all evidence indicates that the Universe is expanding, it must be known when the measurement takes place. One observer here may have a totally different measurement than an observer somewhere else with a different experience of time flow when measuring. An observer in a spacetime framework altered by either velocity-based or gravity-based relativity might see the Universe compressed by the shorter wavelengths of light reaching the observer. An observer with a slowed time experience relative to another observer will see more completed waves with shorter wavelengths in a unit of time. Hence, the light-year will be shorter to the degree that time is slowed in that direction.
This brings up the other question: What is the measuring stick? We have adopted a time-based measurement unit called the light-year. So what started out to be strictly a measurement of space ends up with a time component. A strategy to deal with these uncertainties needs to be adopted if there is ever to be a solution to the radius dilemma.
It will be shown that there is a distinct and knowable radius for the Universe, and that radius is not limited to being a statistical curiosity. It is a fundamental component of the physics of the Universe.
Spacetime Light Cone
Imagine an instantaneous flash of light in open space. The light will expand in a bubble formation at the velocity of light or c. The edge of the light bubble will be at 300,000 kilometers from its source after one second. The bubble will have a radius of cΔt. After two seconds the bubble will have a radius of two light seconds or 600,000 kilometers, and so on.



We now have the beginning of a solution to the radius dilemma. It is necessary to reevaluate what is being measured. The radius is time dependent. The light bulb example shows that the radius of the light bubble is determined by the passage of time. We are not measuring a static quantity. Instead the values derived are of space and the time that it took to enclose the space.
We are not merely calculating the radius of space. We are determining the radius of spacetime. Spacetime is a four-dimensional quantity, and space and time are the four dimensions.
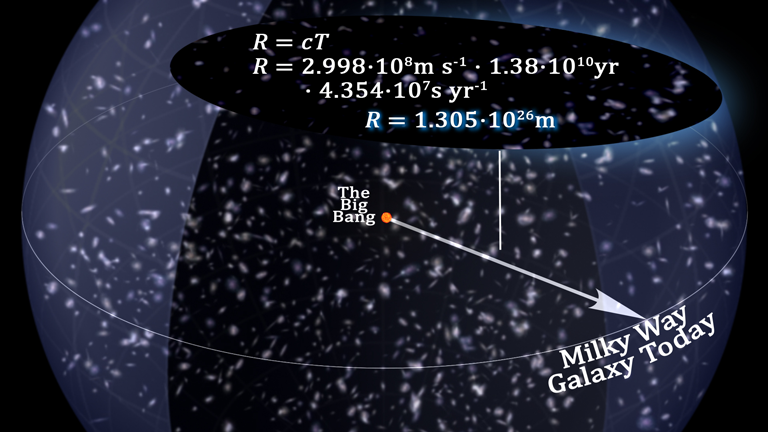
Since the velocity of light is the limiting velocity in the Universe and since light was a major component of the early Universe, then the radius of the Universe is the distance that light can travel for the entire duration of the Universe’s existence. It is estimated that the Universe is 13.98 billion years old.
This age and the current velocity of light results in the following calculation of the Universe’s radius:

Minkowskian Spacetime
Hermann Minkowski, a former teacher of Albert Einstein, determined that a consequence of Special Relativity is that space and time are forever interlinked in something that he called spacetime. Movement in space decreases the rate that a mass moves through time. Observers in different reference frames will see different spatial and time components for the same two events. If the two vantage points have different reference frames, they can be designated by Δt or Δt’, and Δs or Δs’.
In combination, the square root of the summation of the square of the change in space plus the square of the change in time × c between the same events will be equal for all observers, such that:
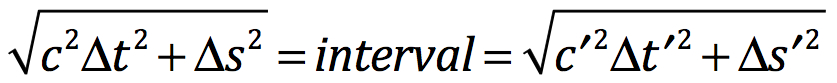
Interval is the absolute within a relativistic universe. Any two events have a unique interval of separation. Each of these events is interconnected to any other event by another interval. And likewise, all of these are interconnected by their own distinct interval. In combination, all events lie in a fixed four-dimensional grid that when taken in its entirety, lays out the history of the Universe.

A worldline is an illustration that plots a mass’ movement in time and space. Typically worldlines are two-dimensional illustrations of the four spacetime dimensions. The three spatial dimensions are substituted for one dimension labeled Δs. The vertical dimension denotes Δt. As time passes, the mass moves up the vertical axis a distance of c × Δt. Tangential movement is movement away from or towards the vertical axis.
The worldline shows movement relative to both space and time. The mass may begin by moving away from the vertical and later back towards the vertical reference line or show acceleration as in Figure 1-4.
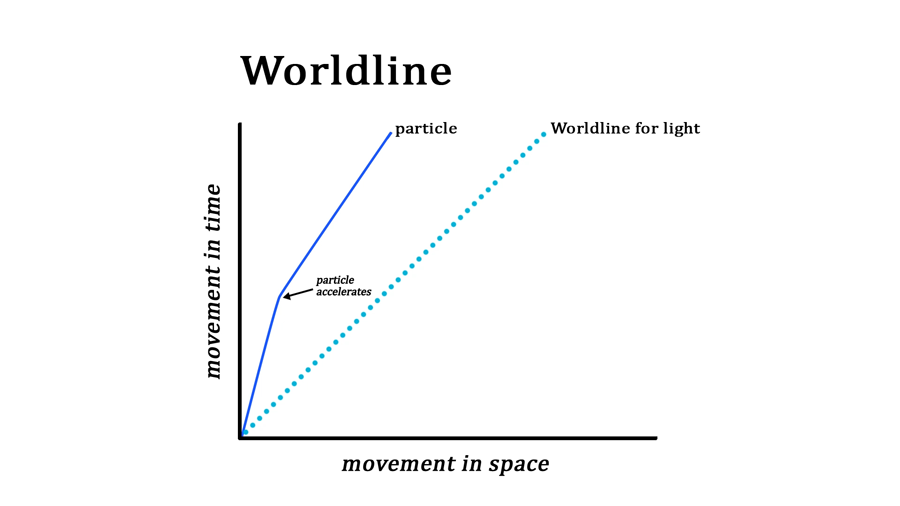
The fastest that energy can move is the velocity of light. The illustration shows the worldline for light. Note that it is a 45º, i.e., it moves forward in space as fast as time passes multiplied by c. All mass-based objects must fall within the 45º angle formed by light.
If a mass just passes through ambient time without a commensurate movement in space, then its spacetime line is directly up the ambient reference line.
If a mass experiences two local events within its internal space separated only by the passage of time, the interval between these two events has no spatial component. Therefore, since Δs = 0, the interval equals cΔt. This interval is referred to as the mass’ worldline. For example, a high-velocity particle when viewed from another reference frame would have a worldline with both time and space components. However, since the particle always exists in the same spatial reference frame relative to itself, it has a strictly time-based worldline.
Every mass in the Universe had its origin in the Big Bang. It is a shared event of all matter. It is at-rest with respect to each mass in the Universe.
The worldline interval between that event and an event in the present moment for every mass is c • Δt. This cannot be over emphasized. Every mass has zero movement relative to itself. Therefore, the passage of time alone is shown in its worldline.
A mass formed in the Big Bang that moves radially away from the Big Bang reference point until the present day is moving in ambient spacetime. Ambient spacetime means that there is no net movement relative to the Universe’s mass other than that due to the expansion of space itself. Ambient spacetime means that it will experience the maximum passage of local time, which is sometimes referred to as wristwatch time. Ambient space represents most of the mass in the Universe since space expands uniformly, and matter usually follows the spokes of the spherical expansion.

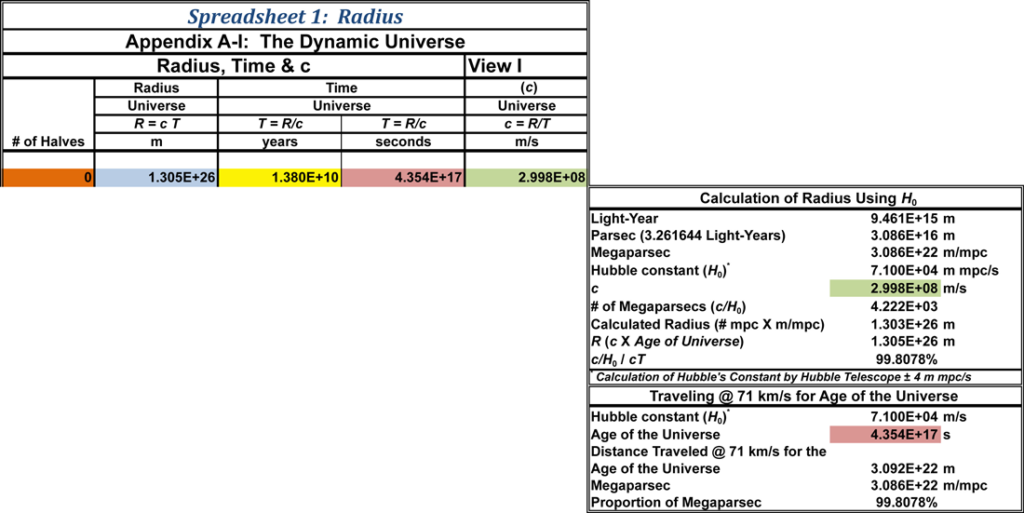
The length of the worldline from the Big Bang is the distance that mass has traveled from that event. This is the largest distance in the Universe and is therefore the Universe’s radius (R). The universal worldline for every mass back to its origin equals R. For this worldline Δt is the age of the Universe, which will be referred to as T. So c • Δt = cT = R. If we assume T to be 13.798 billion years, then R = 1.3798 • 1010 y • 3.155815 • 107 s y-1 • 2.99792458 • 108 m s-1 = 1.30541434 • 1026 meters. From this equation we now have the relationship between the age of the Universe and its size.
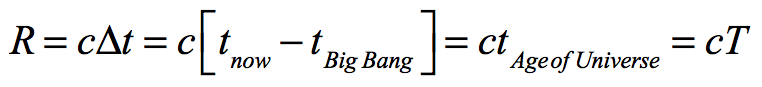
Radius Redefined
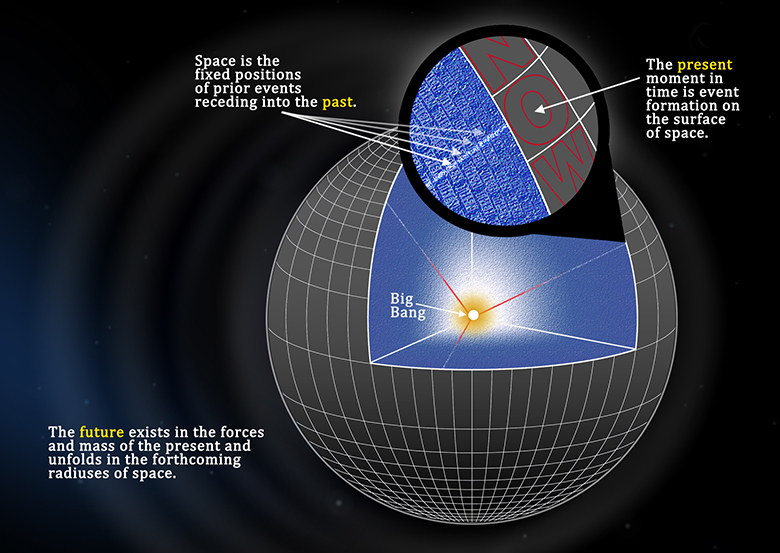
We now have a center from which to measure radius. That center is the Big Bang. The Big Bang is a single point of zero dimensions. Radius formed with the first event forming a sphere with a Planck radius. Each Planck increment of time produces an increase of one Planck unit of radius.
Not only does every mass share a universal origin, they also share a universal present. That ubiquitous present unifies the Universe into one cohesive whole. The present is the edge of the Universe’s spacetime sphere. The distance between the Big Bang origin and the “present” surface is the Universe’s radius.
Hubble’s Constant and Universe’s Radius
Does this approximate reality? Edwin Hubble conclusively proved that the Universe is expanding. Beginning in the 1930s until his death in 1953 he attempted to measure the rate of expansion. The expansion rate for the Universe has been defined as Hubble’s constant (H0). Recent advances in techniques and instrumentation have increased the accuracy of the observed rate of expansion.
A recent estimate of Hubble’s constant is 71±4 km s-1 per megaparsec.1 A parsec is approximately 3.26 light years.2 At large distances, where local gravitational effects are reduced, galactic objects are moving away from each other. The rate that distant objects separate is close to universal since it is a product of the Universe’s expansion.
Hubble’s constant is a calculated value based on red shifts or brightness of standard candles. If astronomical objects are separating at 71 km s-1 per megaparsec, then objects separated by 2 mpc will be moving away from one another at a velocity of 142 km per second.
Since the Universe is expanding at the velocity of light, at what distance will galaxies be separating at c? If c is divided by 71 km s-1/mpc, this should reveal the approximate distance from one end of the Universe to the other where the recession velocity is the velocity of light:
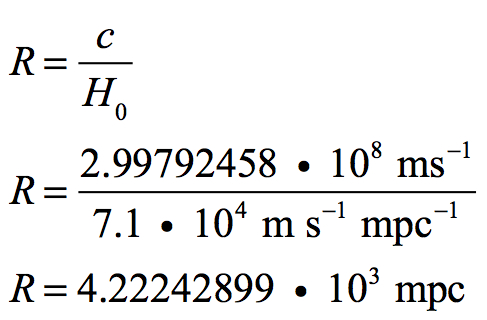
This is equivalent to a radius in meters of:
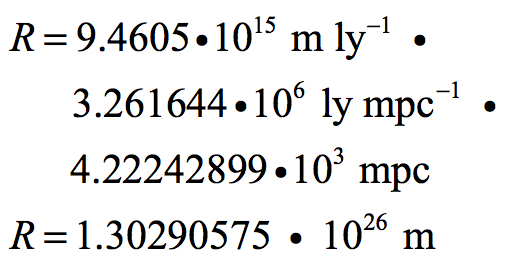
This is exceptionally close to the calculated value of 1.3029 • 1026 meters and is only 0.19% off that value and well within the error limit.
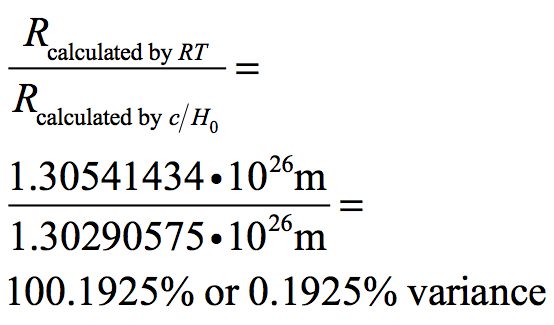
Another way of approaching the problem is to reverse the direction of time and project how much the Universe would compress over the 13.798 billion years of its history. This can be done by multiplying the negative of H0 by the age of the Universe.
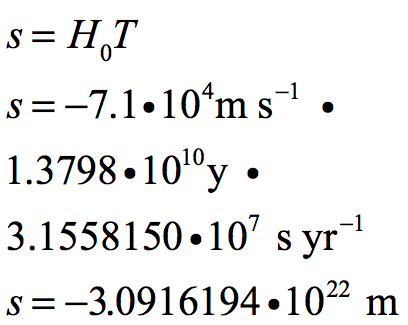
A megaparsec is 3.08567800 • 1022 m. If time was to be reversed and the rate of separation became the rate of consolidation, every mass would arrive at the same location in a time period equal to the age of the Universe. No matter how far apart objects may be, if each megaparsec interval were to compress at 71 km per second for a period of 13.798 billion years, all locations in space would be compressed to a single point. This point was the Big Bang.
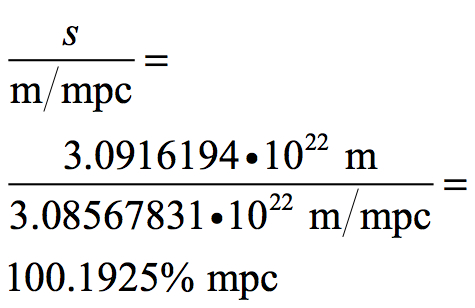
This is a very interesting conclusion. It doesn’t matter how large the Universe is. If every location in space separated by a megaparsec were to reverse direction for the age of the Universe, then all points in the Universe would coalesce at a single location. The difference is that if the Universe is larger than 4,222 megaparsecs, then the final consolidation would be at a velocity greater than the velocity of light.



The Current Estimates
The Universe is seen as having two radii: One is the radius of the visible universe and the other is the radius of the entire universe. The present paradigm for the Universe’s expansion believes that the earliest Universe underwent a hyper-expansion called inflation. This caused the Universe to be of an unspecified but incredible size. A hyper-inflated Universe would have vast regions of unreachable and unseeable space. According to this theory the Universe’s size is completely unknown and dependent upon random oscillations that are perceived to have taken the Universe out of the hyper-inflationary epoch.
Since this theory leaves incredible unseeable regions of space, we are left with assessing the size of what can be seen. There are estimates of the “visible Universe”. These are based upon the distance to the most remote observable galaxies and the expansion since the time that light left these distant sources. Some believe that the visible Universe is 46 billion light-years in radius. Doubling this radius makes the diameter of the visible Universe 91 billion light-years across.
Challenge to the Prevailing Belief
Imagine a grid of points at equal distance from each other exactly one megaparsec separation filling the entire Universe. Visualize spheres one megaparsec in diameter as a series of marbles. If these are laid on a flat surface, six marbles would connect around a central marble. Above this hexagon of marbles three marbles can be placed such that each marble center is exactly one diameter from the central seven marbles. The same can be placed below. If the marbles are now spread out over the surface such that they form a circular layer, another layer can be placed above and below the central layer. If all marbles are grouped such that a sphere can be created, it will be seen that all marble centers are exactly one diameter from the adjacent centers.
Now place these spherical center points in space that are one megaparsec from all adjacent points. If these spheres fill the entire Universe, then a grid of equidistant points would encompass all of space. If we use the assumption that the visible universe is 91 billion light-years in diameter, and if we reverse the movement of spacetime at the Hubble rate of 71 km mpc-1, every megaparsec interval will close at 71 km per second. After 13.798 billion years the points in space will all coalesce at one point that we can label the Big Bang.
Initially, the most distant points in our megaparsec grid will approach each other at a velocity greatly in excess of c. Below is that calculation showing Hubble’s constant multiplied times 91 billion light-years converted to megaparsecs:

This is 6.607 × the velocity of light:

A 91 billion light-year visible universe would have a separation velocity at the extremes of 6.6 times the velocity of light. If time is reversed then the megaparsec grid of points within the universe would shrink at 71 km/s. After 13.798 billion years every grid point would merge with the adjacent grid points. Near the end of this process, all points would be in very proximate space.
This calculation is only for what is seen as the visible universe. According to inflation theory, there is vastly more universe outside of the “visible universe” for which to account. Regardless of how big the Universe is, a ubiquitous Hubble’s constant would in reverse time coalesce the Universe in 13.798 billion years. A universe of trillions of light-years or even, as some have hypothesized, an infinite Universe, would coalesce all megaparsec grid points in 13.798 billion years. An infinite universe would have an infinite approach velocity at its extremes.
This leaves the question: Does Special Relativity apply to this very early universe when all masses were in close proximity to every other piece of matter? Does Special Relativity apply in this situation or is it once again discarded due to some technicality? Why not just discard Special Relativity as having any meaning whatsoever?
Since the Universe is assumed to be isotropic, i.e., similar in all ways throughout the cosmos, distant reaches of the Universe are assumed to obey Hubble’s constant as they do in local space. This means that the greater the distance objects are, the greater is the separation velocity. At a certain distance separation velocities exceed the velocity of light. Due to this reason and due to the beliefs for how black holes behave, it is assumed that light’s speed limit established by Special Relativity only applies to local space. Under these assumptions, Special Relativity becomes limited in a way that Einstein never intended – distance changes the law. This leaves the question: What is the limiting distance for when Special Relativity applies? How close do masses have to be for the law to apply?
For example, if the Universe has an extreme radius of 1050 meters and if every section of space separated by a megaparsec coalesced at 71 km s-1mpc-1, then the extremes of the Universe would approach each other at 7.66 • 1023 times the velocity of light:
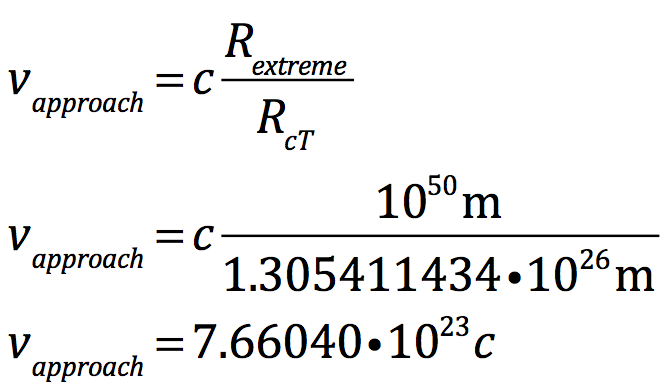
This absurdly large value for approach velocity means that Special Relativity has absolutely no meaning. Masses cannot approach or separate each other faster than c. Today’s paradigm considers Special Relativity as relevant only when the masses are local. After 13.798 billion years of coalescing all mass would be local to each other. The approach velocity cannot be possible. Any size for the Universe larger than the Hubble limit becomes untenable.
Radius from What?
What is radius? What are we measuring? This is where current theory fails. When we observe the Universe, we are observing the past. Distance is measured in light-years. Distance is time based.
The four dimensions of the Universe are the three Euclidean axes and one time-based dimension. Time is a fourth dimension that “can’t be seen all at once”. It is a dimension that comes to us over time. It is depth.
Minkowskian intervals combine movements in space and movements in time. The passage of time alone creates interval. We see depth and that depth is the past. Radius must be redefined as the Minkowskian interval to the most distant point in the past. That point is the Big Bang.
The further objects are from our point of observation; the further they are in the past. We are able to observe the cosmic background radiation from when the Universe was 380,000 years old, but mass and energy before this point exist beyond the CBR veil.
If we imagine total transparency of the early Universe, ask where is the Big Bang itself? Is it up from the observer’s position, to the right, left or down? Since every object in the Universe originated at the Big Bang, then clearly the Big Bang exists radially behind the distant objects that one observes. Since objects exist in all directions, then the Big Bang is the envelope encompassing the entire Universe, receding at the redshift for an object moving at the velocity of light.
This is the radius of the Universe. As space expands, so does the distance between objects. Objects that appear to be 10 billion light-years away were much closer when light left its source. So the expansion is built into the observation. Therefore, the radius of the Universe is literally the distance to the Big Bang.
We are the Minkowskian distance to the Big Bang, and the same applies for every other mass in the Universe. Every mass exists in a common present, and that present is RT from the Big Bang. The volume of the Universe is that of a four-dimensional light cone equal to the age of the Universe.
One-Degree of Freedom Short
Degrees of freedom refer to the ability of an object to move. For example, a ball sitting in a physical well cannot move without the application of force. The ball therefore has zero degrees of freedom. However, if the ball floats in a slot, it has one degree of freedom that we can name as sideways. The second degree of freedom can be added by placing the ball on a plane. That extra movement can be named back and forth.
If we move the ball into a non-barrier bound space, it will have three degrees of freedom. The third degree will be called up and down. These are the three spatial degrees of freedom. These are the three Cartesian coordinates of our observable universe.
It has already been stated that there is no observable edge to the Universe. There is a reason for this. We live one degree of freedom short of the vantage point that would allow us to see the Universe as one cohesive four-dimensional whole. What is the fourth degree of freedom that we lack? That is the spatial aspect of time, i.e., cΔt of the worldline. As already stated, matter exists in the common present. That present limits our vantage point to this moment. It has already been stated that the radius of the Universe is the layers of time before now. We therefore are locked into the single vantage point of the omnipresent NOW. We cannot “ride the radius” to different vantage points for that would mean moving through time.3
One aspect of time can now be defined. Time is a spatial dimension that cannot be seen all at once. In order to see the Universe in all four dimensions one would have to be extra-universe and able to see all time at once in the same way that a spatial dimension can be seen.
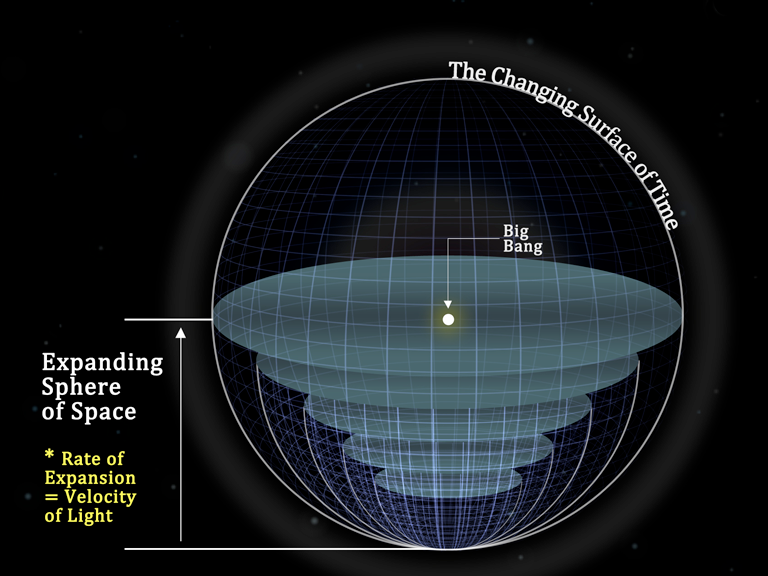
The Four-Dimensional Spacetime Light Cone
Light expands spherically over time as seen with the flash-bulb illustration. This expanding sphere is often referred to as a light cone. It is illustrated in a three-dimensional way by replacing the sphere with a circle and showing a cone with that circle as its base. The height of the cone is the expansion that occurs with the passage of time.
The three-dimensional light cone illustration can be formed by integrating the formula for a circle. This forms a light cone where the height of the cone is the same dimension as the radius of the circle.
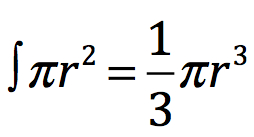
Of course the true light cone is not three dimensional. It is a four-dimensional cone; three of space and one of time. It is an expanding sphere from a single point origin to a sphere advanced forward in time. Just like the formulation for the three-dimensional cone, the four-dimensional cone’s formulation is achieved by the integration of the formula for the volume of a sphere rather than the area of a circle.
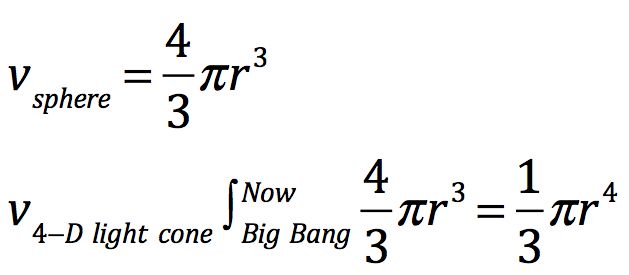
Note that the formula resembles that of the 3-D version. The 4-dimensional light cone is the volume of the Universe’s spacetime. It is all of the time periods of the Universe at once.
The Universe is a four-dimensional experience. We of course can’t see it that way because we are contained within its dimensions. Seeing the Universe in its entirety is “God’s” vantage point. This is not a statement about the existence of God. It is however a statement about a holistic view of all that is part of this place we call our universe.
- There have been other studies that have calculated slightly different values for Hubble’s constant.
- A parsec is a cumbersome unit of measure for astronomical distances. It is based upon the measurement to proximate stars using the parallax of Earth’s orbit.
- I first gained clarity about the “one-degree-of-freedom-short” concept from my good friend Kenneth Nelson.
